DDPM
2025年9月7日
16:23
DDPM:
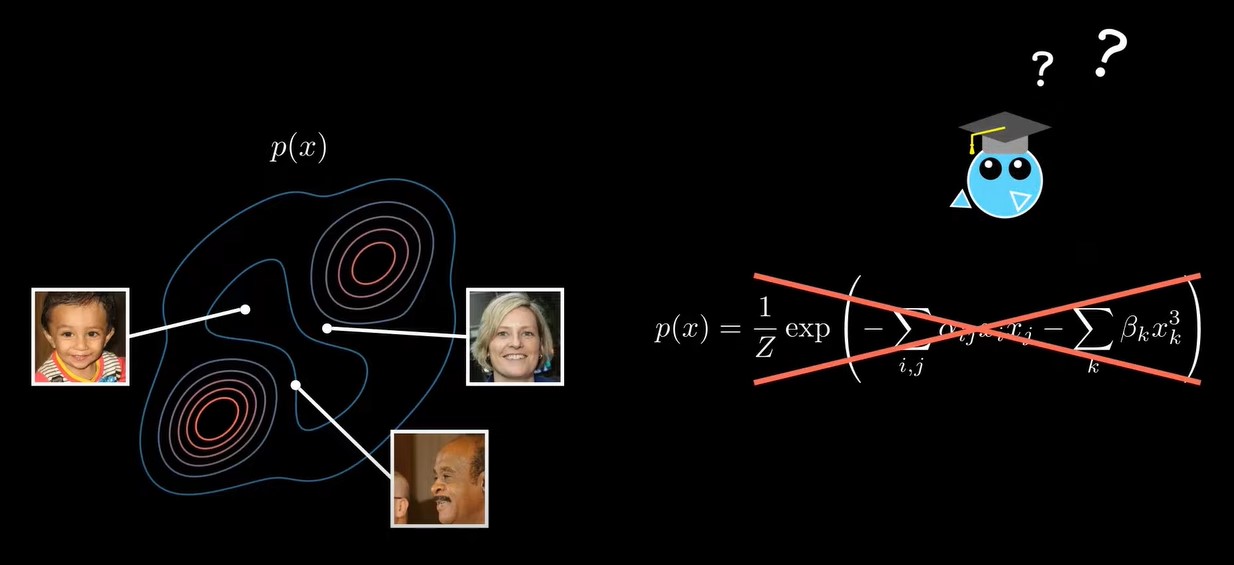
假设我们的数据是人脸数据,这个数据存在一个分布p(x),但是我们不知道这个分布p(x)的具体形式,甚至p(x)有可能是不存在的。但是我们仍然希望能生成新的数据,e.g.从p(x)这个分布中采样 。那么如何在不知道p(x)分布的情况下,从这个分布中采样呢?
扩散模型通过从图片中去掉高斯噪声来解决这个问题。
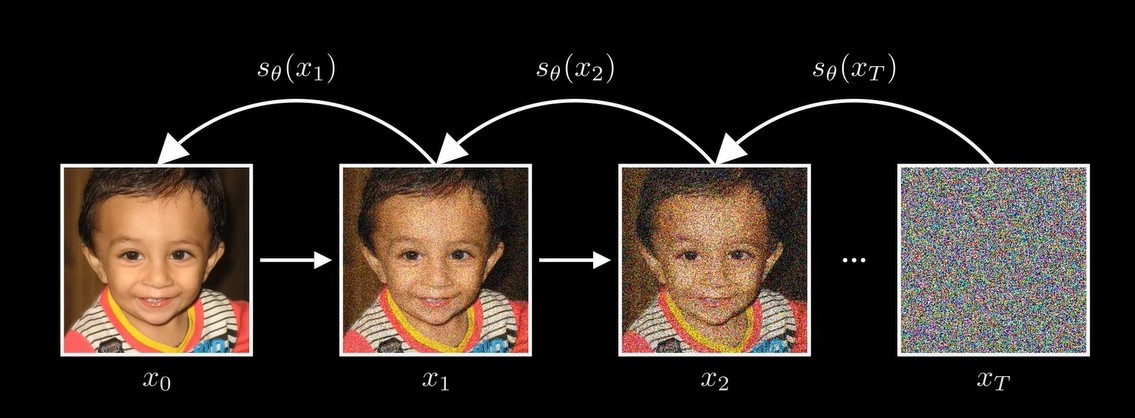
对原始图片,逐步地增加随机噪声,最后得到完全随机噪声的图片,然后训练模型,,逐步地去掉图片中的噪声,恢复图片。![]()
数学形式推导:
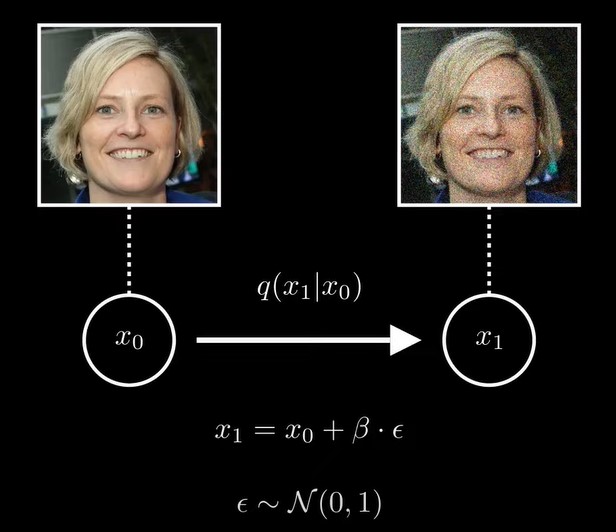
,那么条件概率q(x1|x0)就是一个均值为x0,方差为的高斯分布![]()
![]()
所以,rather than seeing this as adding noise to x0, we can just imagine x1是 we take a sample from a 均值x0,方差为的高斯分布,![]()
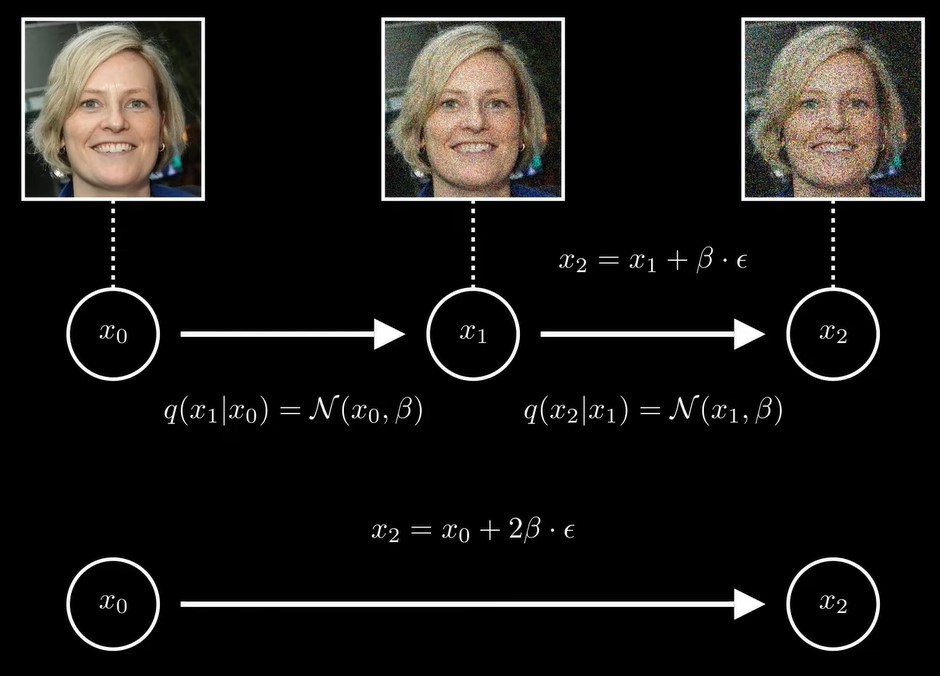
同理,,那么条件概率q(x2|x0)就是一个均值为x0,方差为2的高斯分布,![]()
对于时刻t,

这样的问题是,我们希望时刻t的图片是一个均值为0,方差为1的高斯分布,而不是,,意味着均值一直是x0,方差随着t一直增加,因此,我们需要重新定义这个扩散过程。![]()
很显然,我们需要改变每一步分布的均值,我们在x前面加一个衰减系数,![]()

于是,q(xt|x0)可以写成下面的形式,这样就可以保证,只要大于0小于1,当t趋于无穷时,这个分布的均值收敛到0,方差收敛到1,是一个标准正态分布。![]()
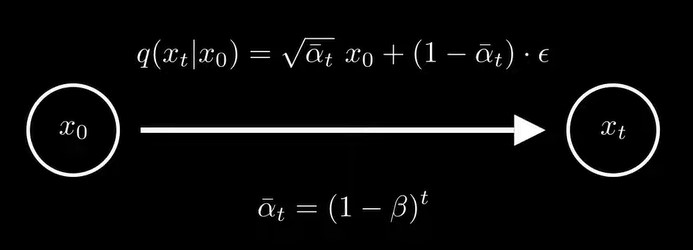
在实际中,在每步时是变化的,有一个schedule,而不是固定的,那么的公式就变成了下图形式,![]()
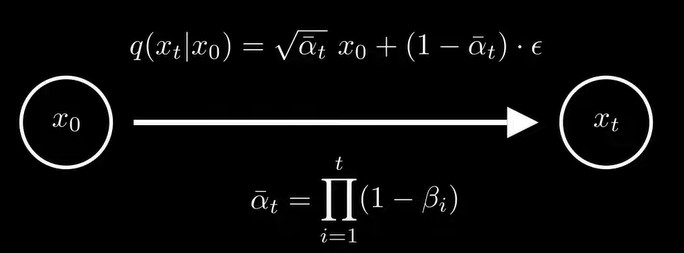
现在,我们定义了一个扩散过程:将一个任意分布变成标准正态分布,
那么如何训练一个神经网络来reverse这个扩散过程呢?
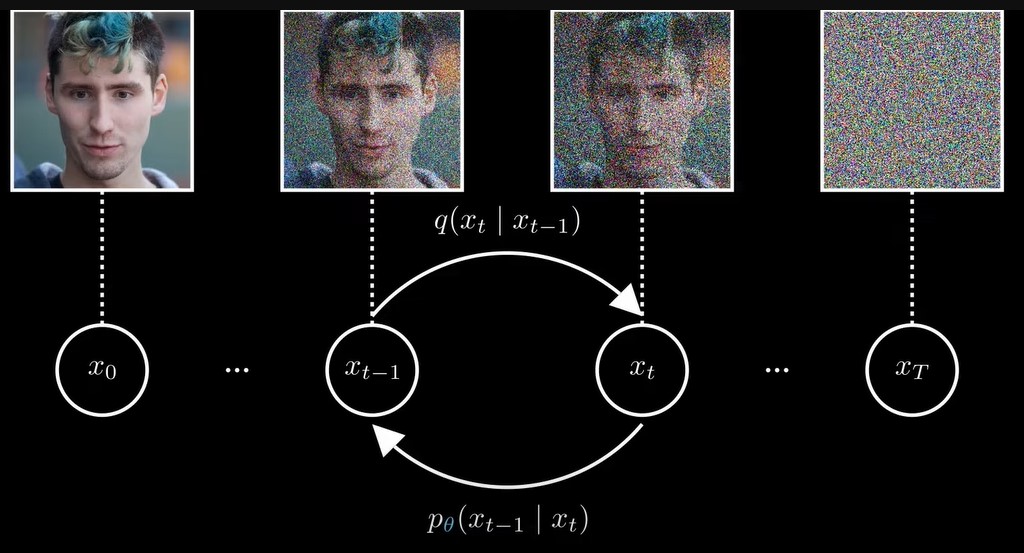
中的就是神经网络中的参数,也就是说,输入一张图片到神经网络,然后神经网络输出另一张图片,这个过程就相当于从这个分布中采样, 中的就是这个分布的参数,神经网络拟合的就是这个分布的参数。![]()
那么,如何训练这个神经网络呢?极大似然!或者说minimize the negative log likelihood of
producing a sample using our nn model. 即minimize ![]()
描述由x0到从x1到xT所有变量的联合概率分布表示了整个前向加噪过程:
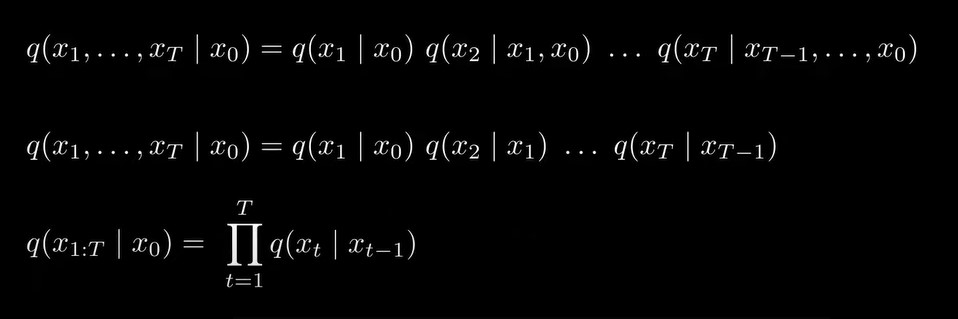
同理,逆向去噪过程的联合概率分布,可以写成:
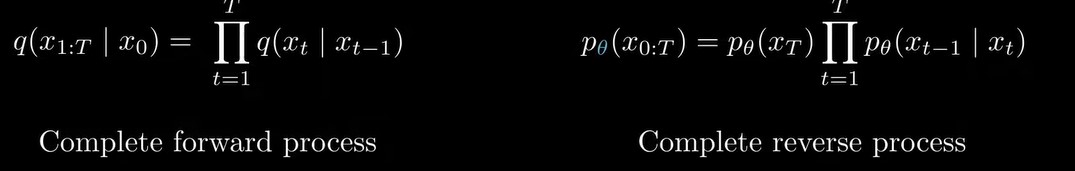
从公式可以看出,逆向去噪过程并没有conditioned(前向过程conditioned on x0),这和实际相符,逆向过程直接从一张高斯噪声图片开始,不需要任何先验,而前向过程要求输入x0。
有了分布之后,现在才看如何得到似然函数的表达式,when dealing with joint probabilities, a useful first step is often to marginalize the distribution with respect to other variables,
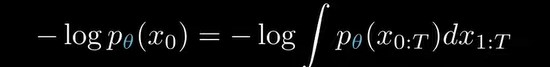
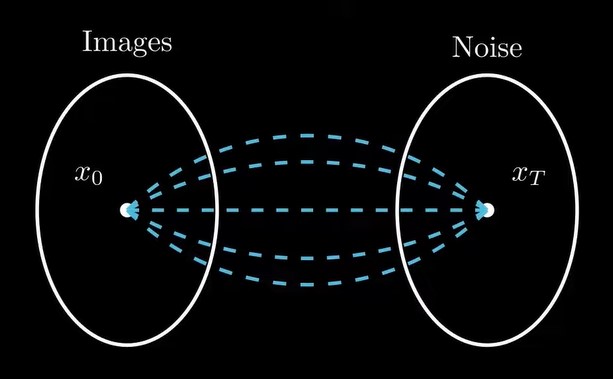
但是我们能用上面这个式子计算得到吗?答案是并不能。上面这个式子表示 ,要得到(神经网络生成图片x0的概率 ),我们需要sum over all possible paths capable of
generating it,如下图所示,这是intractable的。![]()
我们用一个trick,分子分母同乘以前向过程的联合概率分布,并写成期望的形式,由于是convex的,我们可以应用jeson不等式,如下图所示,![]()
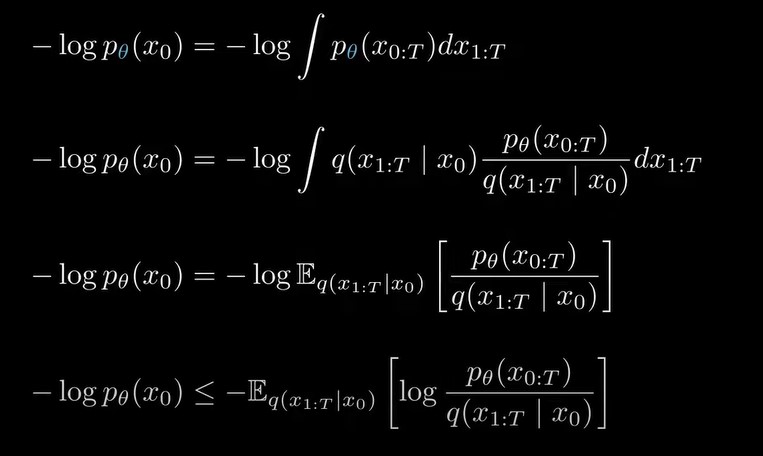
这样,就得到了似然函数的上界ELBO,将ELBO进行重写,(推导过程详见DDPM论文补充材料),
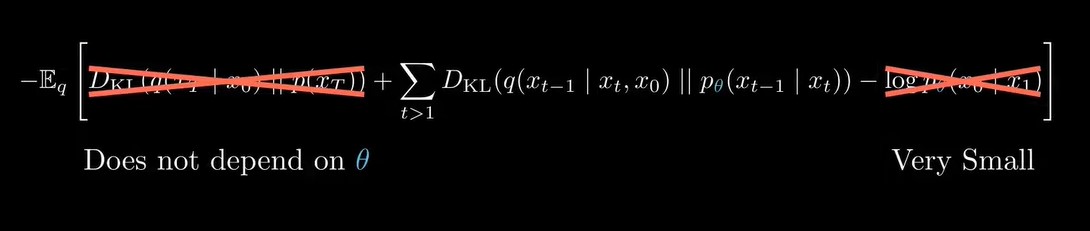
上式也就只剩下中间的的KL散度了,其中是真实后验,这里的q和前向过程中的q(xt|xt-1)不是一个q,如下图所示, conditioned on xt和x0,是逆向过程的真实分布,并且我们是知道这个分布的closed form的形式的。那么既然已经有了逆向过程的解析分布表达式了,为什么还需要神经网络来学习这个分布呢,因为这个真实后验需要我们知道x0,但是在推理时,我们不知道x0,我们的目标就是恢复x0,但是在训练时,我们可以使用x0,从上图可以看出,训练的目标是让神经网络拟合一个分布来逼近真实后验分布,
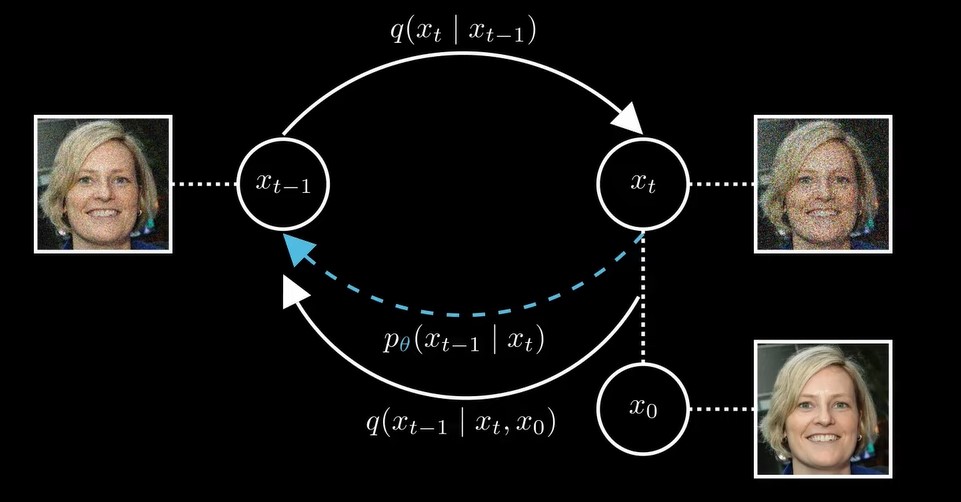
这个分布是高斯的,具体推导省略,那么我们也选择是一个高斯分布的形式,原因1)前向过程是高斯的,所以逆向过程也是高斯分布,更合理,2)高斯分布简洁。于是,我们的神经网络就要拟合这个高斯分布的均值和方差,在实际应用中,通常固定这个分布的方差,只需要拟合均值,也就是让两个分布的均值越接近越好。![]()
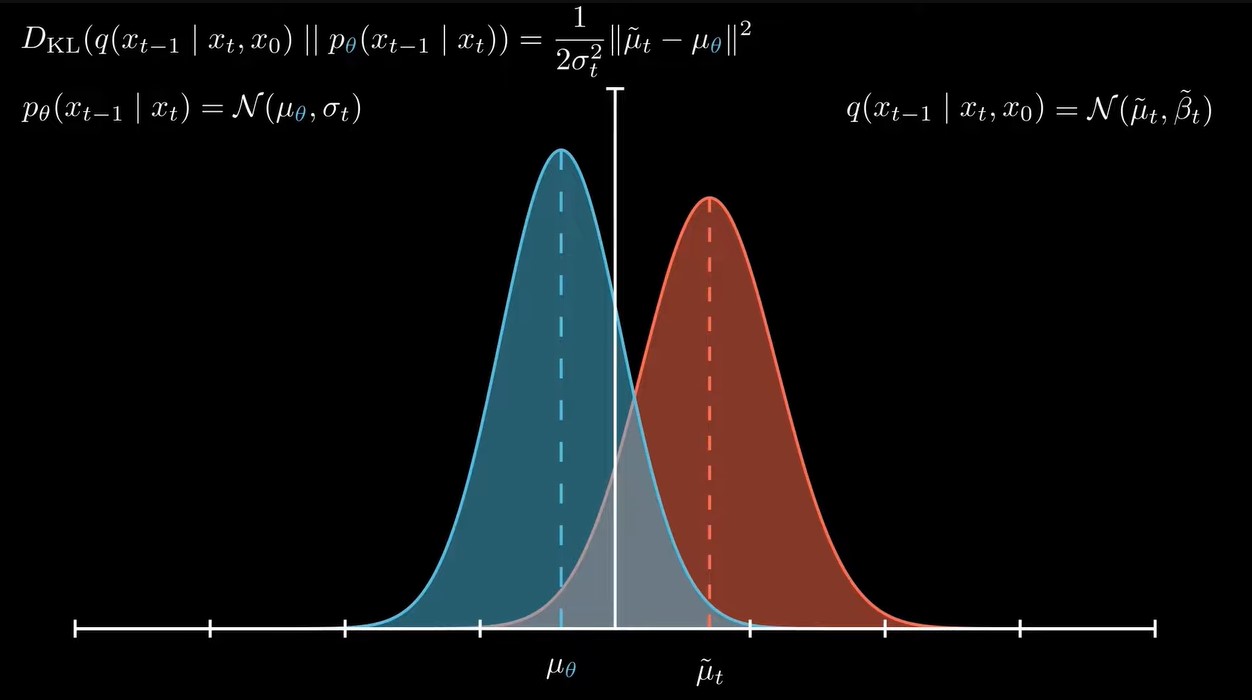
训练的目标也就是拟合每一步的分布的均值,使得每一步的均值更接近真实后验分布的均值
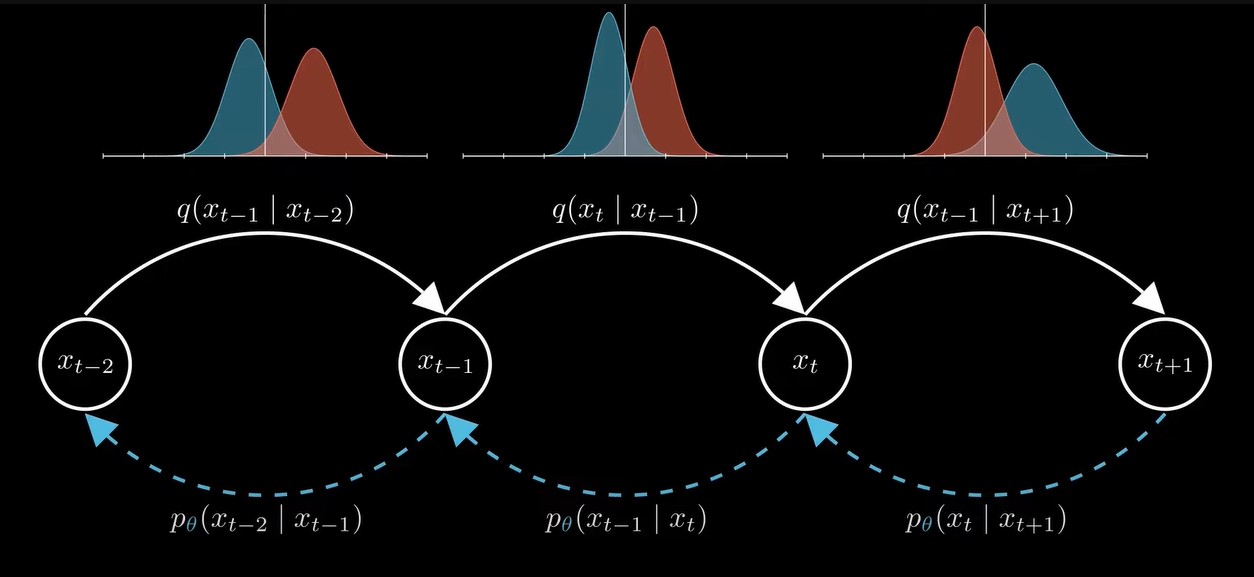
于是,损失函数就变成了下图的形式

将均值换成误差的形式,重写成下图
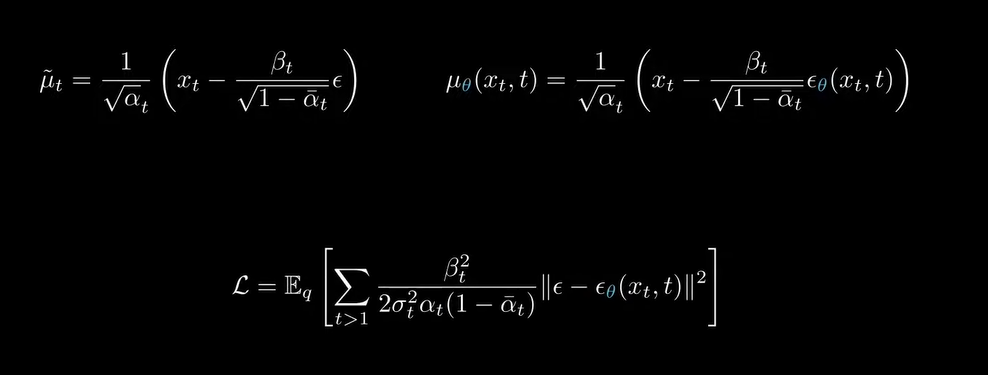
神经网络的拟合目标就变成了第t步时的加的噪声,并对所有t求和。在实际应用中,通常随机挑选出t,而不是对所有的t拟合,最终 的收敛效果是一样的。
训练代码:
import torch
import deepinv
from torchvision import datasets, transforms
device = "cuda"
batch_size = 32
image_size = 32
transform = transforms.Compose(
[
transforms.Resize(image_size),
transforms.ToTensor(),
transforms.Normalize((0.0,), (1.0,)),
]
)
train_loader = torch.utils.data.DataLoader(
datasets.MNIST(root="./data", train=True, download=True,
transform=transform),
batch_size=batch_size,
shuffle=True,
)
lr = 1e-4
epochs = 100
model = deepinv.models.DiffUNet(in_channels=1, out_channels=1,
pretrained=None).to(
device
)
optimizer = torch.optim.Adam(model.parameters(), lr=lr)
mse = deepinv.loss.MSE()
beta_start = 1e-4
beta_end = 0.02
timesteps = 1000
betas = torch.linspace(beta_start, beta_end, timesteps, device=device)
alphas = 1.0 - betas
alphas_cumprod = torch.cumprod(alphas, dim=0)
sqrt_alphas_cumprod = torch.sqrt(alphas_cumprod)
sqrt_one_minus_alphas_cumprod = torch.sqrt(1.0 - alphas_cumprod)
for epoch in range(epochs):
model.train()
for data, _ in train_loader:
imgs = data.to(device)
noise =
torch.randn_like(imgs)
t = torch.randint(0,
timesteps, (imgs.size(0),), device=device)
noised_imgs = (
sqrt_alphas_cumprod[t, None, None, None] * imgs
+
sqrt_one_minus_alphas_cumprod[t, None, None, None] * noise
)
optimizer.zero_grad()
estimated_noise =
model(noised_imgs, t, type_t="timestep")
loss =
mse(estimated_noise, noise)
loss.backward()
optimizer.step()
torch.save(
model.state_dict(),
"trained_diffusion_model.pth",
)
推理代码:
import torch
import deepinv
from pathlib import Path
device = "cuda"
image_size = 32
checkpoint_path = "./checkpoints/trained_diffusion_model.pth"
model = deepinv.models.DiffUNet(
in_channels=1,
out_channels=1, pretrained=Path(checkpoint_path)
).to(device)
beta_start = 1e-4
beta_end = 0.02
timesteps = 1000
betas = torch.linspace(beta_start, beta_end, timesteps, device=device)
alphas = 1.0 - betas
alphas_cumprod = torch.cumprod(alphas, dim=0)
sqrt_alphas_cumprod = torch.sqrt(alphas_cumprod)
sqrt_one_minus_alphas_cumprod = torch.sqrt(1.0 - alphas_cumprod)
model.eval()
n_samples = 32
with torch.no_grad():
x = torch.randn(n_samples, 1,
image_size, image_size).to(device)
for t in
reversed(range(timesteps)):
t_tensor =
torch.ones(n_samples, device=device).long() * t
predicted_noise =
model(x, t_tensor, type_t="timestep")
alpha = alphas[t]
alpha_cumprod =
alphas_cumprod[t]
beta = betas[t]
if t > 0:
noise =
torch.randn_like(x)
else:
noise = 0
x = (1 /
torch.sqrt(alpha)) * (
x - (beta /
torch.sqrt(1 - alpha_cumprod)) * predicted_noise
) + torch.sqrt(beta) *
noise