KL散度

2025年5月31日

17:29

 

1. 自信息（惊喜）：概率的倒数

2. 熵（惊喜的平均值，信息量）：概率*惊喜，用于衡量分布的不确定性大小。

3.交叉熵（ wrong belief下的惊喜的平均值，用另一个分布进行编码的信息损失量）：H(P,Q)是P的概率*Q的惊喜值，H(Q,P)是Q的概率*P的惊喜值，H(P,Q)和H(Q,P)是不同的。 交叉熵也没有对称性。

input = torch.tensor([[ 1.1973,  0.7670, -0.2514,  1.6228, -1.4611],

        [ 0.5193,  0.6425, -1.0573, -0.4303,  0.2234],

        [ 1.4941, -2.3918,  0.3820,  1.0978, -0.6612]], requires_grad=False)

 

target = torch.tensor([[0.0626, 0.2186, 0.3879, 0.2348, 0.0960],

        [0.1350, 0.5222, 0.0936, 0.1046, 0.1446],

        [0.0925, 0.1738, 0.2922, 0.1807, 0.2607]], requires_grad=False)

 

loss = nn.CrossEntropyLoss()

loss(input, target),loss(target, input)

(tensor(1.9742), tensor(0.8449))

 

4.KL散度：和距离不同，KL散度没有对称性，KL(P|Q) = H(P,Q)-H(Q)，KL(Q|P) = H(Q,P)-H(P)，分为前向和后向。

 

对于离散分布的KL散度，需要对所有可能的结果求和，对于语言模型来说，这些可能的结果是vocab中的所有的token，而现代模型可以拥有超过20万个token的vocab；对于连续分布来说，除非是高斯分布，否则 没有闭式解。因此需要一种有效估计KL散度的方法，

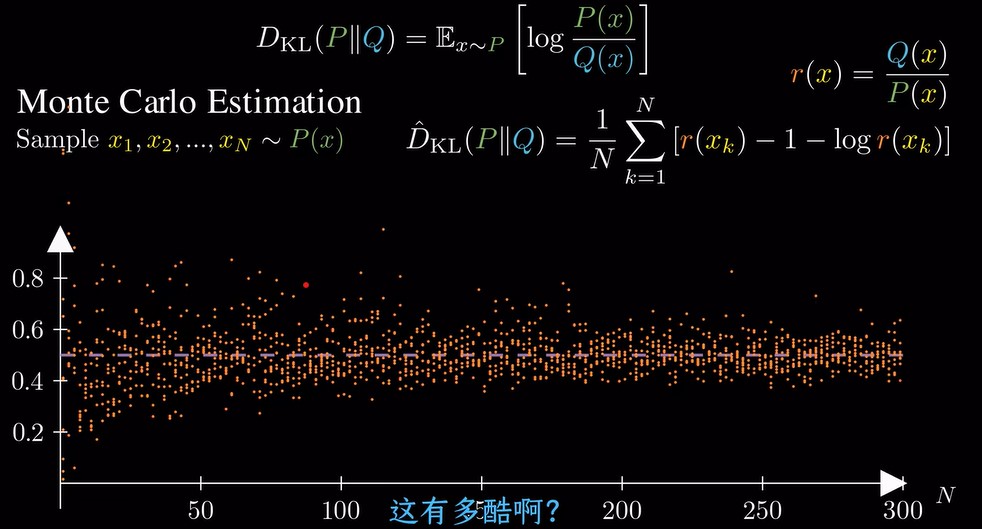
将KL散度写成期望的形式，然后用蒙特卡洛采样，用平均值来估计KL散度。

 

 

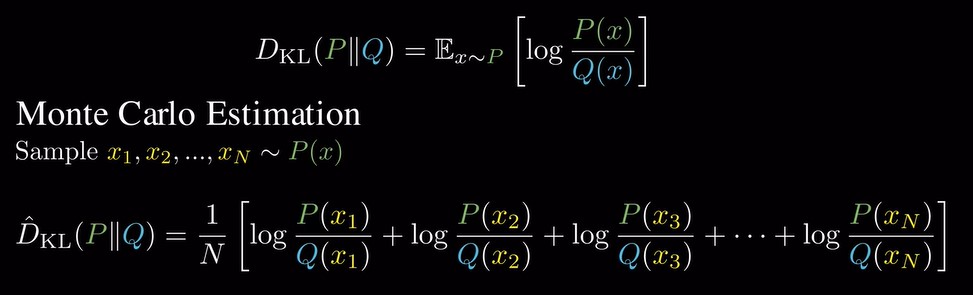
这个估计是无偏的，即偏差很小，但方差很大，如下图所示，

 

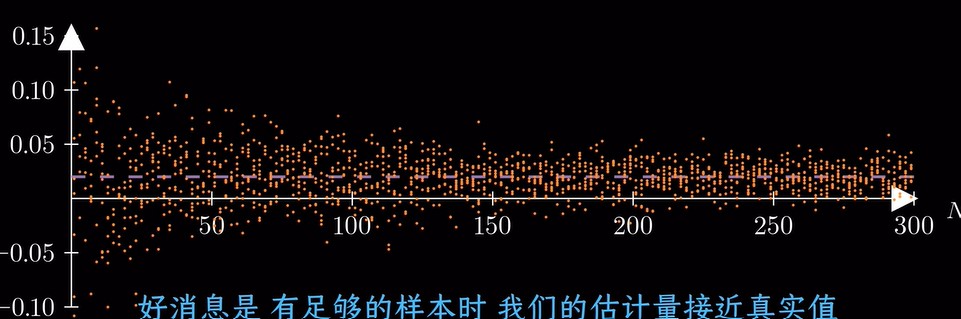
换一种估计方式，偏差大，方差小

 

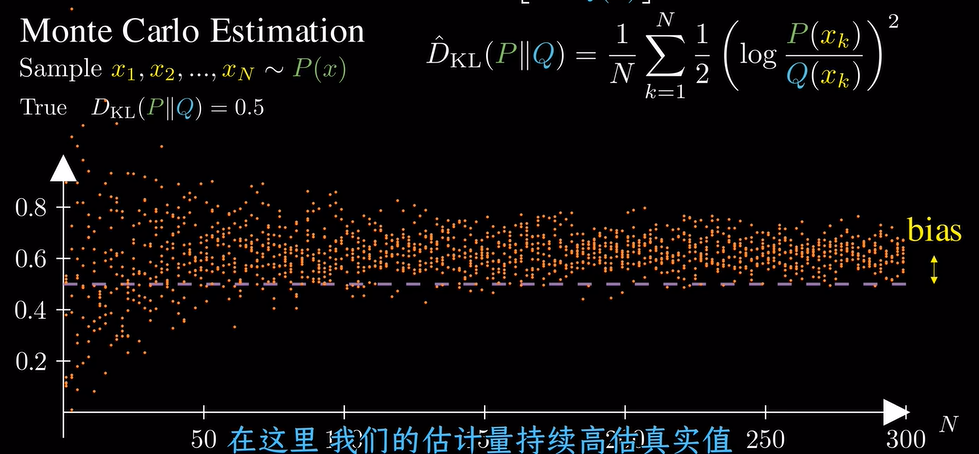
再换一种估计方式，此时偏差和方差都很小，