聚类
2025年10月10日
14:19
Kmeans
- 确定k的大小,类别数量
- 随机选择k个点,作为类别中心点
- 计算每个数据点到k个类别中心的距离,将数据点划到最近的那个类别中去
- 重新计算类别中心点的位置
- 重复步骤3,4,直到类别中心点的位置不再发生变化,或所有样本点的类别不再改变
聚类结果的好坏,可以通过类内的样本方差来确定。
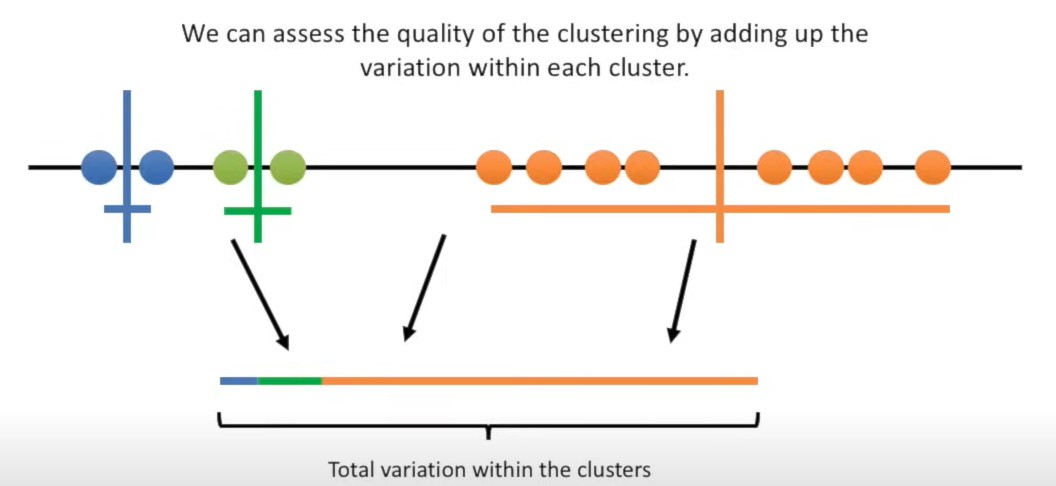
如何找到最优的聚类结果?可以多次选择初始点,选择类内样本方差最小的那次。
如何确定k的大小?
1)如果任务场景确定,如5种类别的消费级别,直接k=5
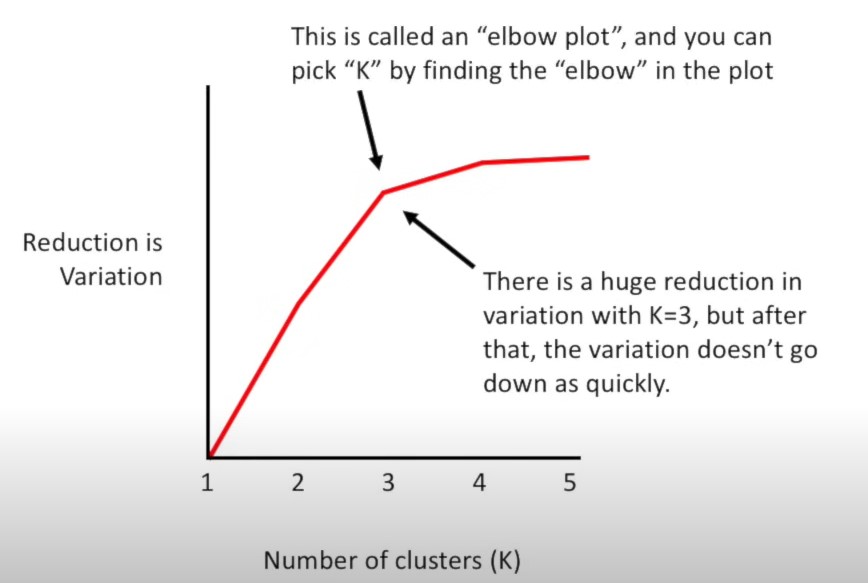
2)尝试k=1,2,3,4…,分别统计类内样本方差,当然k越大,类内方差越小,但是可以看拐点,下图中k=3之后 ,类内方差下降得没有之前那么多,所以k=3。
Hierarchical Clustering
- 计算各聚类之间的距离(初始时,每个数据点是一个单独的聚类)
- 根据距离函数,将最相似的两个聚类合并为一个新的聚类
- 重复步骤1,2,直到所有的数据被合并为一个聚类。
两个类的距离函数:
- 类A中的所有点和类B中的所有点的最小距离 ,距离可以用欧式或曼哈顿
- 类A中的所有点和类B中的所有点的最大距离
- 类A中的所有点和类B中的所有点的平均距离
- 类A和类B中心的距离
优点:
- 不一定需要指定聚类的数量。
- 像 k-means 一样,分层聚类算法很容易实现。
- 它可以输出聚类树(dendrogram)的层次结构,这可以帮助决定聚类的数量。
缺点:
- 分层聚类的主要缺点是其时间复杂性。与其他算法相比,它的复杂度相对较高,为\(O(n^2 \text{log}n)\),n为数据点的数量。
- 一个聚类被创建,成员数据点就不能被移动。(与此相对的是一批 soft clustering 算法)
- 根据距离矩阵的选择,它可能对噪音和异常值很敏感。
hclust 最常见的运用可能还是在各种 heatmap 中展示聚类的情况。
DBSCAN
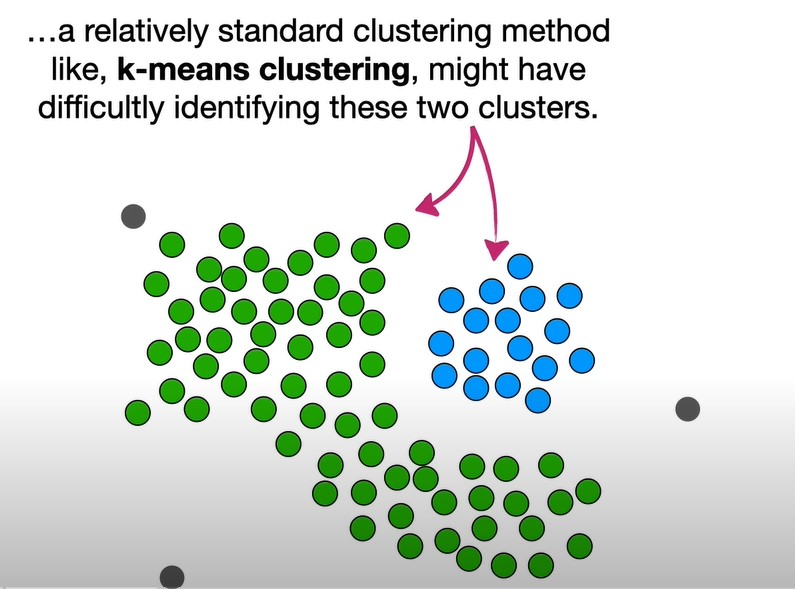
对于上图这种,绿色类别包裹在蓝色类别外面,kmeans聚类无法将这两种类别很好地区别开。
人类用肉眼能轻松看出上图中两个类别 ,是根据密度来看的,dbscan就是根据密度来聚类 的。
DBSCAN 的原理要简单的多,但是这并不意味着它的效果就会差,在很多算法表现不好的非凸数据集上(凸数据集可以简单理解为数据集中的任意两点连线上的点都在数据集内),DBSCAN 往往能取得较好的效果,见下图,这也是 DBSCAN 最大的优势,而且 DBSCAN 还可以作为异常检测算法,发现噪声点(离群点)。
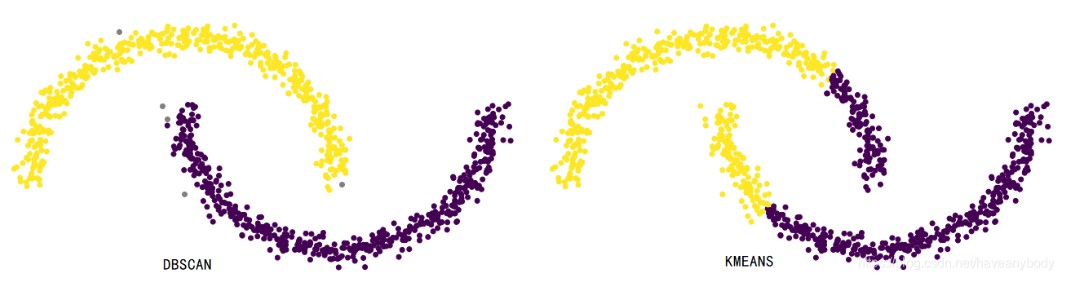
DBSCAN(Density-Based Spatial Clustering of Applications with Noise,具有噪声的基于密度的聚类方法)是一种基于密度的空间聚类算法。该算法将具有足够密度的区域划分为簇,并在具有噪声的空间数据库中发现任意形状的簇,它将簇定义为密度相连的点的最大集合。关于什么是密度相连我们下面解释。
1.1 密度定义
DBSCAN 是基于一组邻域来描述样本集的紧密程度的,参数 (eps, min_samples) 用来描述邻域的样本分布紧密程度。其中,eps 描述了某一样本的邻域距离阈值,min_samples 描述了某一样本的距离为 eps 的邻域中样本个数的阈值。
假设已知样本集\(D = \{x_1, x_2, …, x_m\}\),则 DBSCAN 具体的密度描述定义如下:
- eps - 邻域:对于\(x_j \in D\),其 eps - 邻域包含样本集 D 中与\(x_j\)的距离不大于 eps 的子样本集,这个子样本集的个数记为\(|N \in (x_j)|\),这里需要注意距离并不一定是欧氏距离,具体在 API 章节会再详细介绍。
- 核心对象:核心对象,又叫核心点。对于任一样本\(x_j \in D\),如果其 eps - 邻域对应的\(|N \in (x_j)|\)不小于\(min\_samples\),即如果\(|N \in (x_j)| \geq min\_samples\),则\(x_j\)是核心对象。
- 密度直达:如果\(x_i\)位于\(x_j\)的 eps - 邻域中,且\(x_j\)是核心对象,则称\(x_i\)由\(x_j\)密度直达。注意反之不一定成立,即此时不能说\(x_j\)由\(x_i\)密度直达,除非且\(x_i\)也是核心对象。
- 密度可达:对于\(x_i\)和\(x_j\),如果存在样本序列\(p_1, p_2, p_3, \dots, p_T\),满足\(p_1 = x_i\),\(p_T = x_j\),且\(p_{t + 1}\)由\(p_t\)密度直达,则称\(x_j\)由\(x_i\)密度可达。也就是说,密度可达满足传递性。此时序列中的传递样本\(p_1, p_2, \dots, p_{T - 1}\)均为核心对象,因为只有核心对象才能使其他样本密度直达。注意密度可达也不满足对称性,这个可以由密度直达的不对称性得出。
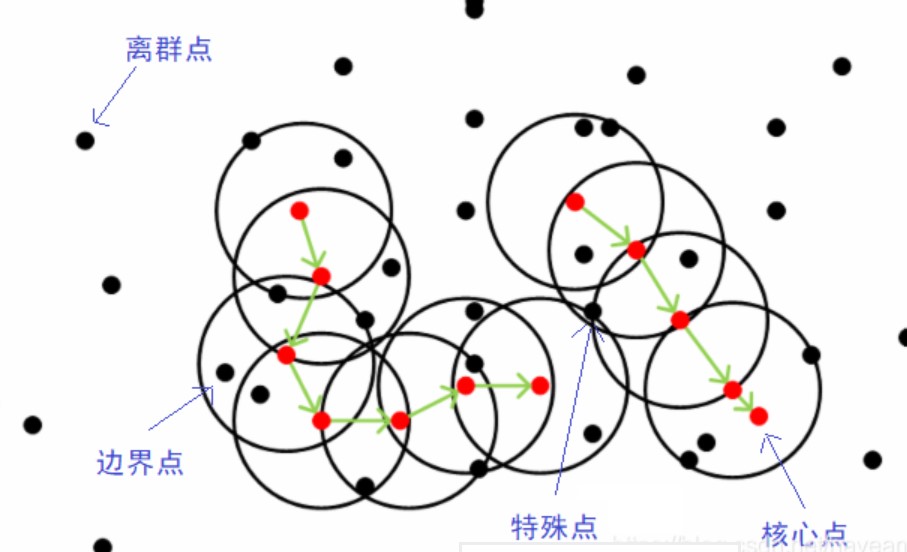
红色的是核心点,也就是至少有min_samples个邻居的点,先选择任意一个未被分类的核心点,如果它的邻居中有其他核心点,就进行扩散,一直进行这个过程,直到邻居中没有核心点,然后将这个类别 中的所有核心点的非核心点邻居也加入到这个类别中。
有了密度定义,DBSCAN 的聚类原理就很简单了,由密度可达关系导出的最大密度相连的样本集合,即为我们最终聚类的一个类别,或者说一个簇。所以任意一个 DBSACN 簇都至少有一个核心对象,如果有多于一个核心对象,则这些核心对象必然可以组成密度可达序列。
那么怎么才能找到这样的簇样本集合呢?DBSCAN 使用的方法很简单,它任意选择一个没有类别的核心对象作为种子,然后找到所有这个核心对象能够密度可达的样本集合,即为一个聚类簇。接着继续选择另一个没有类别的核心对象去寻找密度可达的样本集合,这样就得到另一个聚类簇。一直运行到所有核心对象都有类别为止。参考上图的两个绿色箭头路径,聚类的两个簇。
聚类完成后,样本集中的点一般可以分为三类:核心点,边界点和离群点(异常点)。边界点是簇中的非核心点,离群点就是样本集中不属于任意簇的样本点。此外,在簇中还有一类特殊的样本点,该类样本点可以由两个核心对象密度直达,但是这两个核心对象又不能密度可达(属于两个簇),该类样本的最终划分簇一般由算法执行顺序决定,即先被划分到哪个簇就属于哪个簇,也就是说 DBSCAN 的算法不是完全稳定的算法。这也意味着 DBSCAN 是并行算法,对于两个并行运算结果簇,如果两个簇中存在两个核心对象密度可达,则两个簇聚为一个簇。
根据上面介绍的原理可知,DBSCAN 的主要计算量仍然是在距离上,这里同样可以借鉴 elkan K-means 和 KNN KD 树 / 球树的原理进行优化,减少计算量。
(1) 优点
- 不需要预先指定聚类数量,可以对任意形状的稠密数据集进行聚类,相对的,K-Means 之类的聚类算法一般只适用于凸数据集。
- 可以在聚类的同时发现异常点,对数据集中的异常点不敏感。
- 聚类结果没有偏倚,相对的,K-Means 之类的聚类算法初始值对聚类结果有很大影响。
(2) 缺点
- 如果样本集的密度不均匀、聚类间距差相差很大时,聚类质量较差,这时用 DBSCAN 聚类一般不适合。
- 如果样本集较大时,聚类收敛时间较长,此时可以对搜索最近邻时建立的 KD 树或者球树进行规模限制来改进。
- 调参相对于传统的 K-Means 之类的聚类算法稍复杂,主要需要对距离阈值 eps,邻域样本数阈值 min_samples 联合调参,不同的参数组合对最后的聚类效果有较大影响。eps 越大,得到的簇数也就越少,得到的簇就越大,离群点就越少;min_samples 越大,离群点就越多,得到的簇越小。