Logistic regression

2025年3月24日

16:03

建模：

二分类问题，也就是求二项分布的概率p，由于p取值范围是[0,1]，而线性模型wx+b的取值范围是[-inf,inf]，所以对不直接用线性模型拟合p。Odds=p/1-p，取值范围是[0,inf]，log(odds)的取值范围是[-inf,inf]，因此，用线性模型来拟合log(odds)，然后再将log(odds)转换为p，就得到了分类概率。

将log(odds)转换为p，用到的就是Sigmoid函数，log(odds)也称为logits.

 

策略（定义损失函数）：

用线性回归模型来拟合log(odds)，可以像线性回归一样用mse来优化吗？不可以。因为数据的标签y是0或1，log(odds)就是-inf或inf，也就无法计算mse。

用似然函数作为loss，用线性模型计算得到的log(odds)，转换得到P(x)，似然likelihood =  ，取对数就变成了相加的形式，log(似然)=,   log(似然)即交叉熵损失函数。

 

多分类softmax回归：

同理，多分类即多项式分布，对每个类别c，求P(c).  

P（c)可以理解为 的形式，count的取值范围是[0,inf]，log(count)的取值范围是[-inf,inf]，那么就可以用线性模型来拟合log(count)，log(count)即logits。每个类别都对应一个线性模型。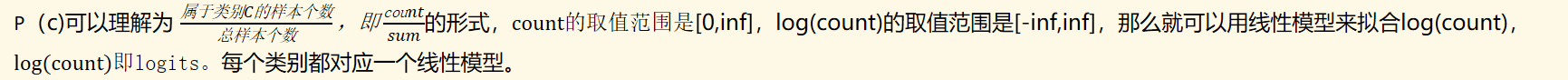

将Log(count)转换为p，用到的就是softmax函数，log(count)即logits。

 

损失函数仍然是似然函数。