位置编码

2025年7月26日

9:21

为什么需要位置编码position encode?

假设文本序列是 this is awesome , 每个单词是一个token，现在计算第三个token awesome 的attention value，awesome的attention value等于awesome和序列中三个token的attention score乘以相应token的value，即awesome的attention value = awesome和this的 attention score * this的value + awesome和is的 attention score * is的value + awesome和awesome的 attention score * awesome的value，其中awesome和this的 attention score = dot_product(awesome的query, this的key) ，awesome的query和this的key只与awesome和this的embedding有关，this的value也只与this的embedding有关，即awesome和this的 attention score * this的value只与awesome和this的embedding有关，同理，awesome和is的 attention score * is的value 只与awesome和is的embedding有关，awesome和awesome的 attention score * awesome的value只与awesome的embedding有关。也就是说，awesome的attention value只与 this, is , awesome三个token的embedding有关。那么当文本序列变成 this awesome is时，此时awesome的attention value不会发生变化 ，因为这三个token的embedding没有变化，因此，需要在token的embedding中加入token的位置信息。

 

1.正弦-余弦位置编码

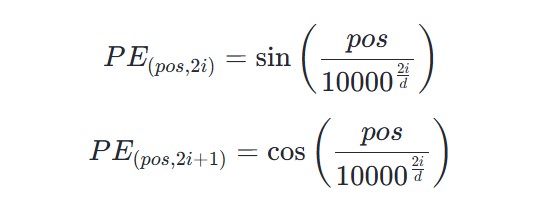
pos表示输入序列的位置索引，d表示embedding的维度，i表示embedding的位置索引。

三角函数的周期为embedding位置索引来决定， 随着i的增加，函数的频率会降低，周期变长，也就是embedding后面的维度的周期要长，振荡缓慢。

pos相当于是三角函数cos(x)的中的x。

正余弦位置编码具有远程衰减性质：对于两个相同的词向量，如果它们的位置距离越近，它们的内积分数越高，反之越低。随着q,k之间距离的增加，它们的内积分数震荡衰减。

正余弦位置编码是绝对位置编码，但是三角函数的数学性质使其也能够捕捉一些相对位置信息，具体来说：距离相近的位置，位置编码的差异小，距离相远的位置，位置编码的差异大（远程衰减）。

 

2.ROPE

通过绝对位置编码的方式实现了相对位置编码。

不对token embedding加入位置信息position embedding，而是对q和k注入位置信息（绝对位置编码），如果注入位置信息后的q和k，它们的内积可以表示为它们之间相对距离m-n的函数，那么就相当于将相对位置m-n引入到了q和k的内积计算中了，实现了相对位置编码。对不同位置的q,k向量进行不同角度的旋转，刚好满足这个性质。

 

对向量qm旋转m\theta个角度，即对向量q左乘一个旋转矩阵：

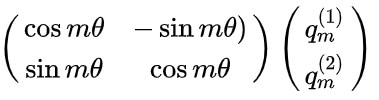
对向量km旋转m\theta个角度，即对向量k左乘一个旋转矩阵：

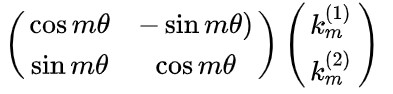
对施加了旋转矩阵后的qm,和kn,进行向量点积，m和n表示token的位置：

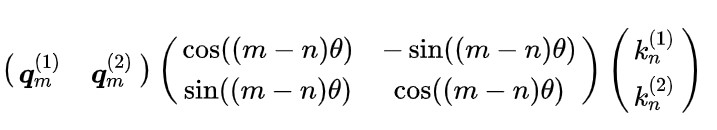
扩展到多维，分成d/2个组，每组进行旋转，每组旋转的基础角度\theta不同，维度低的基础旋转角度大，维度高的基础旋转角度小(和正余弦编码的\theta类似)。

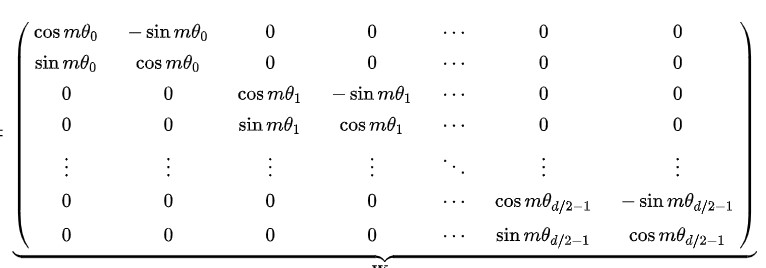
实现方式有2种：

1）转到复数域，llama

xq，xk，xv都是4维的，(B,  T, n_head， head_dim)

xq, xk = apply_rotary_emb(xq, xk, freqs_cis)

 

def apply_rotary_emb(

    xq: torch.Tensor,

    xk: torch.Tensor,

    freqs_cis: torch.Tensor,

) -> Tuple[torch.Tensor, torch.Tensor]:

    xq_ = torch.view_as_complex(xq.float().reshape(*xq.shape[:-1], -1, 2)) #把最后一维拆分成2个维度，原来xq是(B,  T, n_head， head_dim)，现在reshape(*xq.shape[:-1], -1, 2)后是(B,  T, n_head， head_dim//2， 2)，将最后这个维度的两个数，看成是复数的实部和虚部，也就是将q向量head_dim个维度进行两两组合，组合成head_dim//2个组，每个组是一个2维向量，然后将这个2维向量用复数表示，a*(B,  T, n_head， head_dim//2），仍然是4维张量。

    xk_ = torch.view_as_complex(xk.float().reshape(*xk.shape[:-1], -1, 2)) #对k也进行同样的操作，

                                           k的shape(B,  T, n_head， head_dim//2）

    freqs_cis = reshape_for_broadcast(freqs_cis, xq_) #将freqs_cis 的shape是（1，T，1，head_dim//2）

    xq_out = torch.view_as_real(xq_ * freqs_cis).flatten(3) #xq_*freqs_cis是张量对应元素相乘，每个元素都是复数，两个复数相乘，第一个复数是q，第二个复数的模为1，角度为/theta，相当于对q进行旋转\theta，旋转后得到仍然是复数，shape是(B,  T, n_head， head_dim//2），再经过view_as_real，将复数变为实数，shape变成了(B,  T, n_head， head_dim//2，2），再经过flatten(3)，从第3维开始拍扁，shape变成了(B,  T, n_head， head_dim）,变回了xq原始的形状了。

    xk_out = torch.view_as_real(xk_ * freqs_cis).flatten(3)

    return xq_out.type_as(xq), xk_out.type_as(xk)

 

def precompute_freqs_cis(dim: int, end: int, theta: float = 10000.0):

    freqs = 1.0 / (theta ** (torch.arange(0, dim, 2)[: (dim // 2)].float() / dim)) #freqs即上图中的0,1,……(d/2-1)

                                                #freqs是一维张量，长度为dim/2，这里的dim是d_head，即d_model//n_head

    t = torch.arange(end, device=freqs.device)  # type: ignore  #t是一维张量，[0,1,2,…,end]，end是序列最大长度，即T

    freqs = torch.outer(t, freqs).float()  # type: ignore #t和freqs进行torch.outer()，即向量中的每一个元素与另外一个向量中的每一个元素相乘，得到是个矩阵，size是（T，dim/2），矩阵的第[i,j]个元素表示的是第i个token，第j组dim的旋转角度。

    freqs_cis = torch.polar(torch.ones_like(freqs), freqs)  # complex64 #将矩阵转化为复数形式，shape不变，freqs_cis的shape还是（T，dim/2），只不过每个元素是复数，用极坐标表示即模长都为1，角度仍然是freqs 中的角度。

    return freqs_cis

 

def reshape_for_broadcast(freqs_cis: torch.Tensor, x: torch.Tensor):

    ndim = x.ndim

    assert 0 <= 1 < ndim

    assert freqs_cis.shape == (x.shape[1], x.shape[-1])

    shape = [d if i == 1 or i == ndim - 1 else 1 for i, d in enumerate(x.shape)] #将freqs_cis  reshape成xq_的形状，shape是（1，T，1，head_dim//2）

    return freqs_cis.view(*shape)