强化学习的数学原理-第3课

2025年11月21日

16:42

Bellman 最优公式

 

bellman公式，对应某个policy　π，

bellman最优公式,对应最优的policy π*

 

先求解最优policy π*

════════════════════════════════════════════════════════════════════════════════════════════════════

 

最优policy的定义：

对于任意状态s，最优Policy的状态值都大于其他所有policy。

 

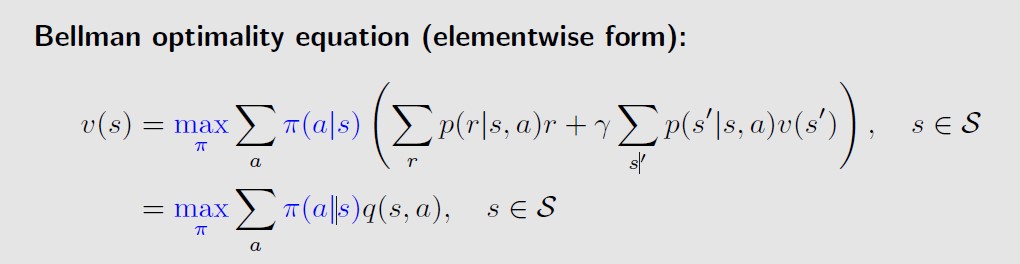
bellman最优公式，就是比bellman公式前面多了个max π，

bellman最优公式的矩阵形式：

那么，求解bellman最优公式，其实需要求出两个量，一个是最优策略π*，一个是最优策略对应的状态值

求解的思路如下，

沿用这个思路，上图中的a对应的就是policy，x对应的是最优状态值，那么就先来求最优时的Policy，

也就是先固定最优状态值，来求policy

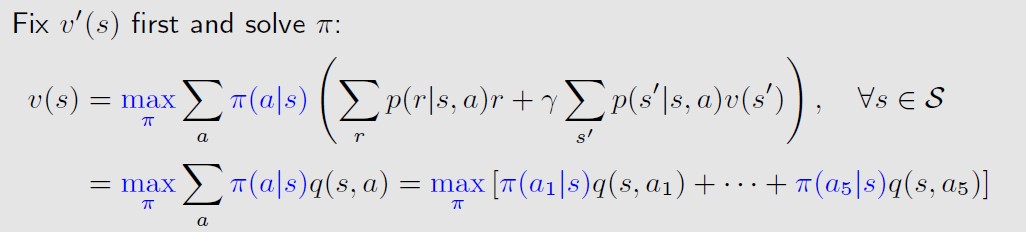
（假定对于状态s，有5种可能 的action），

如何求得状态值max时对应的policy呢，思路如下，

 

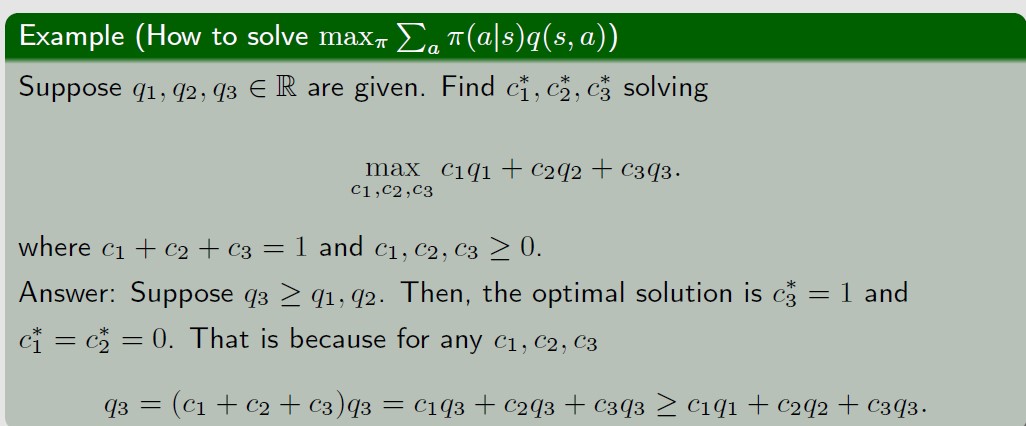
也就是， 要让(c1q1+c2q2+c3q3)最大化，就要让c3=1，c1和c2=0，也就是说，最大化时对应的policy

就是p(q3|s)=1（已知q3>q2和q1）。即最优策略就是选择让state action value q(s,a)最大的那个action a*，

选择这个acton a*的概率是1，其他的action的概率都是0。这个策略是deterministic的，没有随机性。

 

 

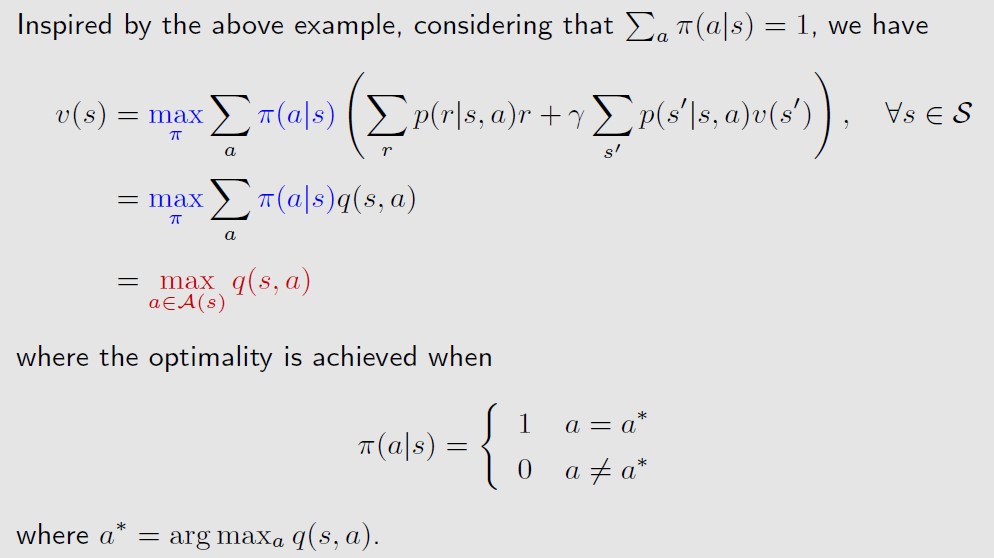
再求解最优状态值v*

════════════════════════════════════════════════════════════════════════════════════════════════════

 

bellman（最优）公式可以写成向量的形式，

 

也就是v=f(v)的形式，其中，v和f(v)都是向量

对应v=f(v)这种形式，用contraction mapping therom来求解

 

 

 

Contraction mapping theorem：如果 f是个contraction mapping，那么有且只有一个fixed point x*，满足f(x*)=x*，并且x*可以通过迭代求解（不断通过x_k+1 = f(x_k)来迭代）。（具体证明过程省略）

 

那么对于向量形式的bellman最优公式，

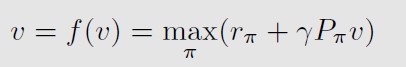
可以证明f是个contraction mapping，即

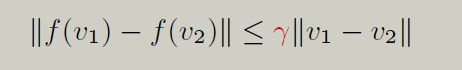
证明过程见《强化学习的数学原理》书中。

 

 

最优分析

════════════════════════════════════════════════════════════════════════════════════════════════════

What factors determine the optimal state value and optimal policy?

最优policy和最优state value是由什么决定的呢，由下图中红色的部分决定

 

着重分析r和ϒ

对于r来说，将r进行affline 变换，a*r +b，不会改变最优策略，只会改变最优状态值的大小

对于ϒ来说，ϒ越大，越远视，ϒ越小，越近视（看重最近的reward，忽略未来的reward）。并且由于

ϒ的存在，设计reward时不需要考虑最优策略会不会有detour的情况，因为只要绕路，那么reward就有会

有ϒ的discount打折，状态值肯定不如不绕路的策略。