强化学习的数学原理-第4课

2025年11月24日

9:21

值迭代和策略迭代(在已知模型表达式的情况下求最优policy)

 

值迭代

════════════════════════════════════════════════════════════════════════════════════════════════════

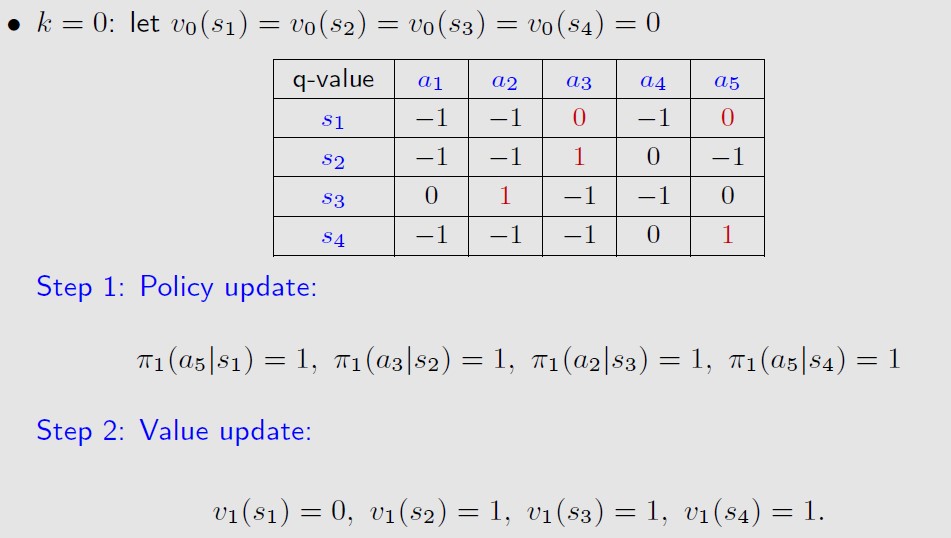
先更新policy，再更新value

用vk计算出所有的state action value q(s,a)，π_k+1就是选择所有q(s,a)最大的那个a。

然后再用π_k+1来得到v_k+1，由于π_k+1就是选择所有q(s,a)最大的那个a，那么v_k+1

就是最大的那个q(s,a)

 

 

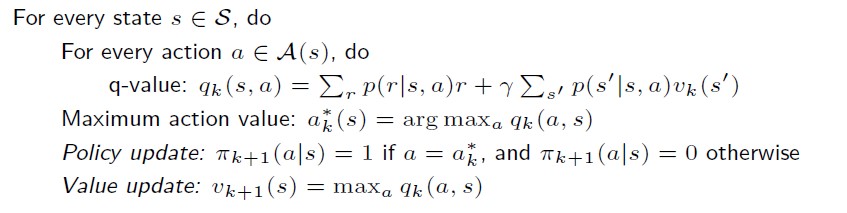
策略迭代

════════════════════════════════════════════════════════════════════════════════════════════════════

 

初始化π0，然后进行policy evaluation得到v，再进得policy improvment得到π1….迭代下去

 

Q1：在policy evaluation时，如何求v？

在policy evaluation时，也就是已知policy，求v，可以用迭代的方法。也就是在policy evaluation

这一步，也需要迭代来求解v（外部迭代算法的内部嵌套了迭代算法）。

 

Q2：在policy improvment时，为什么π_k+1好于π_k？

Q3：为什么这个迭代算法能得到最优策略？

收敛，并且收敛到最优策略，证明过程见书

 

Truncated policy iteration

════════════════════════════════════════════════════════════════════════════════════════════════════

值迭代和策略迭代主要有2个步骤不一样：

1）在上图步骤2中，在初始化第一个v时，值迭代是直接用一个值初始化v0，策略迭代是先初始一个策略π0，然后通过迭代求解bellman公式得到v_π0

2）在上图步骤4中，得到新的策略π1后，值迭代是直接用v0来代入公式得到v1，策略迭代还是要迭代求解bellman

公式得到v_π1

 

这么来看，其实最主要的区别就一个，就是在求解value的时候，值迭代直接用上一步的value代入公式，得到新的

v；策略迭代把上一步的value舍弃了，重新迭代求解bellman公式，得到新的v。

 

Policy iteration在迭代求解bellman公式得到新的v时，也是需要初始化v0，然后一步一步迭代直到收敛，

每一步如下图

那么value iteration就想，反正迭代求解bellman公式也是用vk来求得vk+1，但是需要迭代无穷步，那么我

只迭代一步，得到近似解就行了（反正外层还有个迭代），

 

truncated policy iteration就是介于value iteration只走一步和policy iteration走无穷步之间的，走中间步，

从下图可以看到，truncated的收敛速度介于policy 和value iteration之间。因为在k相同时，policy iteration

实际上进行了更多的计算（迭代求解bellman公式），而value iteration没有迭代求解v。