激活函数

2025年9月15日

16:35

1. Relu

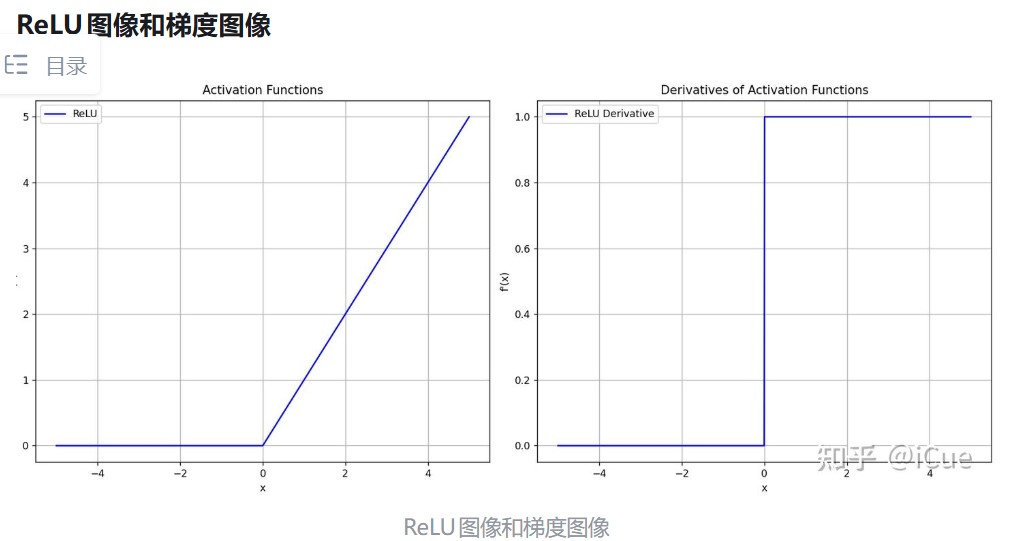
ReLU优点

(1) 计算高效​​：ReLU 的计算仅需判断输入是否大于零，没有复杂的指数运算（如 Sigmoid/Tanh），因此在训练和推理时速度极快

 

​​(2) 缓解梯度消失问题​​：传统激活函数（如 Sigmoid）在输入较大或较小时会进入“饱和区”，梯度接近零，导致反向传播时梯度消失（Vanishing Gradient，ReLU 在正区间（x>0）的梯度恒为 1，避免了梯度消失问题，使得深层网络更容易训练

 

ReLU缺点

​​ (1) 神经元失活（Dead Neurons）​​:当输入为负数时，ReLU 的梯度为零。如果某个神经元在训练中始终输出负数（例如权重初始化不当或学习率过高），其梯度将永远为零，导致该神经元永久失效（“死亡”）, 这种现象称为 ​​Dying ReLU Problem​​

 

 

2. GeLU

 

 

GELU的理解

概率视角​​：GELU将输入 x 的激活权重与其在正态分布中的概率相关联。例如：

当 x 较大时，神经元以高概率被激活（输出接近 x）

当 x 较小时，神经元以低概率被激活（输出接近0）

​​随机正则化​​：GELU的非线性可以被视为一种“自适应Dropout”，其权重由输入自身决定，而非固定概率。

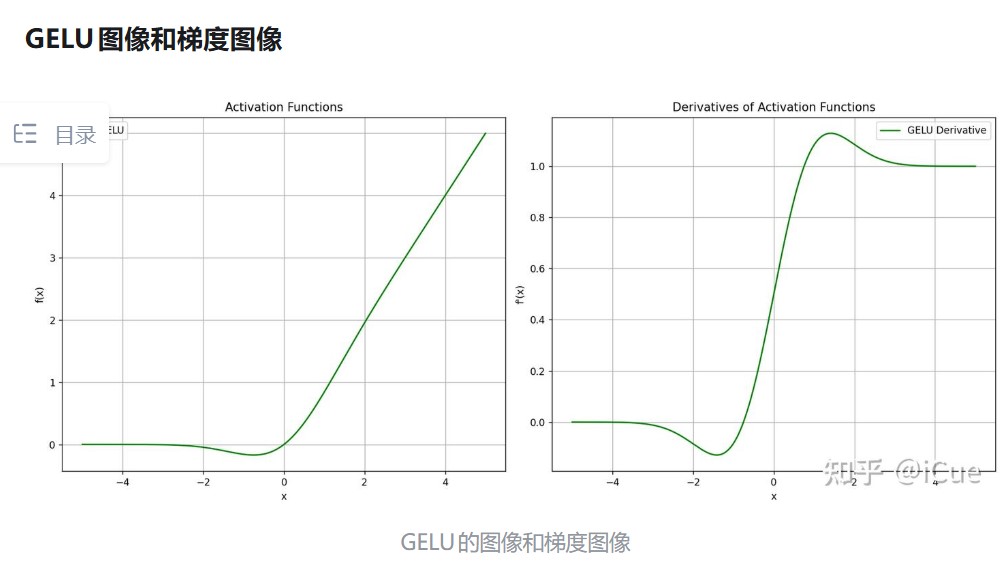
GELU优点

平滑性​​：GELU在输入接近零时是​​连续可导​​的（与ReLU的硬截断不同），这使得梯度更新更稳定

​​自适应激活​​：激活权重 Φ(x) 随输入动态调整，能更好地捕捉复杂模式

GELU缺点

计算成本较高​​: 精确计算 Φ(x) 需要积分运算，尽管近似方法（如tanh或Sigmoid）可以缓解这一问题

 

 

3. Swish

Swish的理解

Swish 对输入 x 进行 Sigmoid 加权，输出范围为 (−0.278,+∞)

当 β→0 时，Swish 退化为线性函数 x / 2​

当 β→+∞ 时，Swish 趋近于 ReLU（x⋅σ(βx)≈x⋅阶跃函数）

Swish的优点

平滑非单调性（Smooth Non-Monotonicity）​​

---​​非单调性​​：当 x<0 时，Swish 可能先减小后增大，与 ReLU 的硬截断不同

​​----平滑性​​：Swish 处处可导，梯度变化连续，缓解了 ReLU 在 x=0 处的梯度突变问题

​​自适应性​​

----通过调整 β，Swish 可以灵活适应不同任务：

​​----大 β​​：接近 ReLU，适合需要稀疏激活的任务（如分类）

​​----小 β​​：接近线性，适合需要保留更多信息的任务（如回归）

​​ 缓解梯度消失​​

----在负区间（x<0），Swish 的梯度非零，避免了 ReLU 的“神经元死亡”问题

​​输出非零中心化​​

----Swish 的输出均值为正（类似 ReLU），可能需搭配 ​​Batch Normalization​​ 使用以加速训练

Swish的缺点

计算成本略高于 ReLU（需计算 Sigmoid）

 

 

4. SiLU

SiLU（Sigmoid Linear Unit）​​，也称为 ​​Swish-1​​，是一种结合了 ​​Sigmoid 函数平滑性​​ 和 ​​ReLU 稀疏激活特性​​ 的激活函数，它由 ​​Swish 激活函数​​ 的特定形式演化而来（固定参数 β=1）

 

 

5. 门控机制