L1范数为什么可以获得稀疏解
L1正则化即在原始的代价函数后面加上一个L1正则化项:
$$
C=C_0+\frac{\lambda }{n}\sum \left | w_i \right |
$$
对新的代价函数求梯度,
$$
\frac{\partial C}{\partial w_i}=\frac{\partial C_0}{\partial w_i}+\frac{\lambda }{n}sgn(w_i)
$$
其中,
$$
sgn(w_i)=\begin{matrix}
1, & if &w_i>0 \\
-1,&if & w_i<0
\end{matrix}
$$
权重$w_i$的更新规则为
$$
w_i^{'} \rightarrow w_i-\frac{\eta \lambda }{n}sgn(w_i)-\eta \frac{C_0}{w_i}
$$
角度1:新的更新规则比原始的更新规则多出了$-\frac{\eta \lambda }{n}sgn(w_i)$这一项,当$w_i$大于0时,更新后的$w^{'}_i$后变小;当$w_i$小于0时,更新后的$w^{'}_i$后变大。因此效果就是让$w_i$往0靠。
角度2:当$w_i$从负半轴趋向于0时,$sgn(w_i)<0$,所以$\frac{\partial C}{\partial w_i}=\frac{\partial C_0}{\partial w_i}-\frac{\lambda }{n}sgn(w_i)$,因此只要有$\frac{\lambda }{n}>\frac{\partial C_0}{\partial w_i}$,就有$\frac{\partial C}{\partial w_i}$小于0;当$w_i$从正半轴趋向于0时,$sgn(w_i)>0$,所以$\frac{\partial C}{\partial w_i}=\frac{\partial C_0}{\partial w_i}+\frac{\lambda }{n}sgn(w_i)$,因此只要有$\frac{\lambda }{n}>-\frac{\partial C_0}{\partial w_i}$,就有$\frac{\partial C}{\partial w_i}$小于0。因此只要保证$\frac{\lambda }{n}$大于原始损失函数在0点处的导数$\frac{\lambda }{n}>|\frac{\partial C_0}{\partial w_i}|$,那么新的损失函数在0点左右的导数就是异号的,即$w_i=0$是极小值点。
由于当$w=0$时,$|w|$是不可导的,实际编程时,可以设$sgn(0)=0,sgn(w>0)=1,sgn(w<0)=-1$
L2范数为什么可以防止过拟合
L2正则化就是在代价函数后面再加上w的L2范数:
$$
C=C_0+\frac{\lambda }{2n}\sum \left | w_i^2 \right |
$$
权重$w_i$的更新规则为
$$
\begin{align}
w_i^{'} \rightarrow &w_i-\frac{\eta \lambda }{n}w_i-\eta\frac{C_0}{w_i} \\
&= (1-\frac{\eta \lambda }{n})w_i-\eta\frac{C_0}{w_i}
\end{align}
$$
在不使用L2正则化时,求导结果中w前系数为1,现在w前面系数为 1−ηλ/n ,因为η、λ、n都是正的,所以 1−ηλ/n小于1,它的效果是让$w_i$变为原来的 1−ηλ/n,那么,虽然权值不断变小,但是因为每次都等于上一次的1−ηλ/n,所以很快会收敛到较小的值但不为0。这也就是权重衰减(weight decay)的由来。当然考虑到后面的导数项,w最终的值可能增大也可能减小。
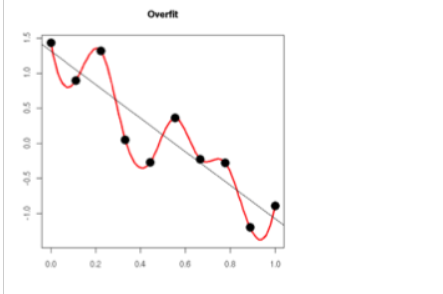
为什么w“变小”可以防止overfitting?
(引自知乎):
过拟合的时候,拟合函数的系数往往非常大,为什么?如下图所示,过拟合,就是拟合函数需要顾忌每一个点,最终形成的拟合函数波动很大。在某些很小的区间里,函数值的变化很剧烈。这就意味着函数在某些小区间里的导数值(绝对值)非常大,即系数足够大。