PCA

优化目标

假设数据集中有m个样本，每个样本有n个特征，那么可以构建一个$n\times m$阶的矩阵$X$，若找到一个$r\times n$阶的矩阵$P$，令$Y=P\times X$，则$Y$是一个$r\times m$阶的矩阵，若r<n，就达到了降维的目的。
从矩阵乘法的角度来解释一下，矩阵$P$的阶数是$r\times n$，这个矩阵的意义是原始空间有n个基向量（每个基向量都由一个n维的向量表示），经过$P$的变换后，每个基向量都由一个r维的向量表示，即将n维空间的向量变换到r维空间中，实现了维度变换。
那么如何得到最优的$P$呢？？（即如何选择这r个基呢？）

内积与投影

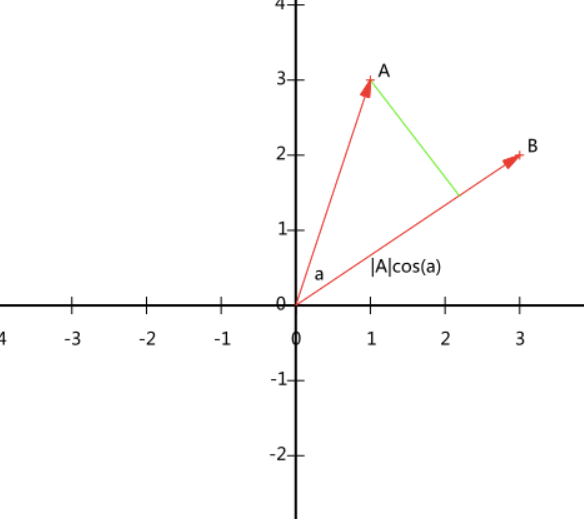
以二维向量为例，设向量B的模为1，则A与B的内积值等于A向B所在直线投影的矢量长度 。
回到n维空间中，现在我们有m个n维向量，我们要做的是在n维空间中找到r个基向量，将这m个向量分别投影到这r个基向量上，然后用投影值表示原始记录。
如何选择这r个基向量的方向才能尽量保留更多的原始信息呢？一种直观的看法是：希望投影后的投影值尽可能分散。

方差与协方差

数学上可以用方差来表示数据的分散程度，一个字段x的方差表示为
$$
Var(x)=\frac{1}{m}\sum_{i=1}^{m}(x_i-\mu )^2
$$
假设已经将每个字段均值都化为0了，那么方差变为
$$
Var(x)=\frac{1}{m}\sum_{i=1}^{m}x_i ^2
$$
于是上面的问题转化为：寻找r个n维基，使得所有数据变换为这r个基上的坐标表示后，方差值最大。
但是问题来了，对于高维空间，首先我们找到一个方向使得投影后方差最大，这样就完成了第一个方向的选择，继而我们选择第二个投影方向。如果我们还是单纯只选择方差最大的方向，很明显，这个方向与第一个方向应该是“几乎重合的”，显然这样的维度是没有用的。因此，应该有其他约束条件。从直观上来说，让两个字段尽可能表示更多的原始信息，我们是不希望它们之间存在（线性）相关性的，因为相关性意味着两个字段还是完全独立，必然存在重复表示的信息。
数学上用两个变量的协方差表示其线性相关性，由于已经让每个字段的均值为0，则协方差为：
$$
Cov(a,b)=\frac{1}{m}\sum_{i=1}^{m}a_ib_i
$$
至此，我们得到了降维问题的优化目标：将一组n维向量降为r维，其目标是选择r个单位(模为1)基，使得原始数据变换到这组基上后，各字段两两间协方差为0，字段的方差尽可能大。

计算方案

协方差矩阵

最终要达到的目的与字段内方差及字段间协方差有密切关系。仔细观察发现，二者均可以表示为内积的形式，而内积又与矩阵相乘有关，于是我们来了灵感：
设我们有m个n维记录，用矩阵形式表示为：
$$
X=\begin{bmatrix}
x_{11} & x_{12} & \cdots &x_{1m} \\
\vdots & \vdots & \vdots & \vdots \\
\vdots & \vdots & \vdots & \vdots\\
x_{n1}&x_{n2} &\cdots &x_{nm}
\end{bmatrix}
$$
然后我们用X乘以X的转置，并乘以系数1/m：
$$
\frac{1}{m}XX^T=\begin{bmatrix}
\frac{1}{m}\sum_{i=1}^{m}x_{1i}^2 & \frac{1}{m}\sum_{i=1}^{m}x_{1i}x_{i2} & \cdots & \frac{1}{m}\sum_{i=1}^{m}x_{1i}x_{in}\\
\frac{1}{m}\sum_{i=1}^{m}x_{1i}x_{i2} & \frac{1}{m}\sum_{i=1}^{m}x_{2i}^2 & \cdots & \vdots \\
\vdots& \vdots & \ddots &\vdots \\
\frac{1}{m}\sum_{i=1}^{m}x_{1i}x_{in} & \cdots & \cdots & \frac{1}{m}\sum_{i=1}^{m}x_{ni}^2
\end{bmatrix}
$$
奇迹出现了！这个矩阵是一个对称矩阵，对角线上的元素是每个字段的方差，而其它元素是两两字段之间的协方差，两者被统一到一个矩阵。

协方差矩阵对角化

根据上述推导，我们发现要达到优化目前，等价于将协方差矩阵对角化：即除对角线外的其它元素化为0，并且在对角线上将元素按大小从上到下排列，这样我们就达到了优化目的。这样说可能还不是很明晰，我们进一步看下原矩阵与基变换后矩阵协方差矩阵的关系：
设原始数据矩阵X对应的协方差矩阵为C，而P是一组基按行组成的矩阵，设Y=PX，则Y为X对P做基变换后的数据。设Y的协方差矩阵为D，我们推导一下D与C的关系：
$$
\begin{align}
D &= \frac{1}{m} YY^T\\
&= \frac{1}{m}(PX)(PX)^T\\
&=\frac{1}{m}PXX^TP^T\\
&=P(\frac{1}{m}XX^T)P^T\\
&=PCP^T\\
\end{align}
$$
现在事情很明白了！我们要找的P不是别的，而是能让原始协方差矩阵对角化的P。换句话说，优化目标变成了寻找一个矩阵P，满足$PCP^T$是一个对角矩阵，并且对角元素按从大到小依次排列，那么P的前K行就是要寻找的基，用P的前K行组成的矩阵乘以X就使得X从N维降到了K维并满足上述优化条件。
现在所有焦点都聚焦在了协方差矩阵对角化问题上，有时，我们真应该感谢数学家的先行，因为矩阵对角化在线性代数领域已经属于被玩烂了的东西，所以这在数学上根本不是问题。

由上文知道，协方差矩阵C是一个是对称矩阵，在线性代数上，实对称矩阵有一系列非常好的性质：

1）实对称矩阵不同特征值对应的特征向量必然正交。

2）设特征值$\lambda$重数为r，则必然存在r个线性无关的特征向量对应于$\lambda$，因此可以将这r个特征向量单位正交化。

由上面两条可知，一个n行n列的实对称矩阵一定可以找到n个单位正交特征向量，设这n个特征向量为$\boldsymbol{e_1},\boldsymbol{e_2},...,\boldsymbol{e_n}$，我们将其按列组成矩阵：
$$
E=(\boldsymbol{e_1},\boldsymbol{e_2},...,\boldsymbol{e_n})
$$
则对协方差矩阵C有如下结论:
$$
E^TCE=\Lambda =\begin{pmatrix}
\lambda_1& & & \\
& \lambda_2 & & \\
& & \ddots & \\
& & & \lambda_n
\end{pmatrix}
$$
其中$\Lambda$为对角矩阵，其对角元素为各特征向量对应的特征值（可能有重复）。
到这里，我们已经找到了需要的矩阵P：
$$
P=E^T
$$
P是协方差矩阵的特征向量单位化后按行排列出的矩阵，其中每一行都是C的一个特征向量。如果设P按照$\Lambda$中特征值的从大到小，将特征向量从上到下排列，则用P的前K行组成的矩阵乘以原始数据矩阵X，就得到了我们需要的降维后的数据矩阵Y。

PCA算法

总结一下PCA的算法步骤：

设有m条n维数据。

1）将原始数据按列组成n行m列矩阵X

2）将X的每一行（代表一个属性字段）进行零均值化，即减去这一行的均值

3）求出协方差矩阵$C=\frac{1}{m}XX^T$

4）求出协方差矩阵的特征值及对应的特征向量

5）将特征向量按对应特征值大小从上到下按行排列成矩阵，取前k行组成矩阵P

6）$Y=PX$即为降维到k维后的数据

进一步讨论

根据上面对PCA的数学原理的解释，我们可以了解到一些PCA的能力和限制。PCA本质上是将方差最大的方向作为主要特征，并且在各个正交方向上将数据“离相关”，也就是让它们在不同正交方向上没有相关性。

因此，PCA也存在一些限制，例如它可以很好的解除线性相关，但是对于高阶相关性就没有办法了，对于存在高阶相关性的数据，可以考虑Kernel PCA，通过Kernel函数将非线性相关转为线性相关，关于这点就不展开讨论了。另外，PCA假设数据各主特征是分布在正交方向上，如果在非正交方向上存在几个方差较大的方向，PCA的效果就大打折扣了。

最后需要说明的是，PCA是一种无参数技术，也就是说面对同样的数据，如果不考虑清洗，谁来做结果都一样，没有主观参数的介入，所以PCA便于通用实现，但是本身无法个性化的优化。

参考

PCA数学原理

关于实对称矩阵的一些性质

1. 实对称矩阵A属于不同特征值的特征向量互相正交
   证明：
   $$
   A\alpha _1=\lambda_1 \alpha _1(1),A\alpha _2=\lambda_2 \alpha _2(2)\\
   (1)\rightarrow \alpha _2^TA\alpha _1=\alpha _2^T\lambda _1\alpha _1 \rightarrow \\
   (A\alpha _2)^T\alpha _1=\alpha _2^T\lambda _1\alpha _1 \rightarrow\\
   \lambda _2\alpha _2^T\alpha _1=\lambda _1\alpha _2^T\alpha _1\overset{\lambda _1\neq \lambda _1}{\rightarrow} \\
   \alpha _1\ and \ \alpha _2 orthogonal
   $$

2. 设A为实对称矩阵，则一定存在正交矩阵Q，使得$Q^TAQ=Q^{-1}AQ$为对角阵
   证明：
   从矩阵的特征基变换的角度来考虑（即如果能找到n个正交的特征向量，就可以将这n个正交向量作为新基，那么矩阵A在这个新基的描述下就是对角矩阵的形式）。已知矩阵A属于不同特征值的特征向量相互正交，属于同一特征值的不同特征向量线性无关，那么可以对这些线性无关的向量做施密特正交化，转化为相互正交的向量，由于施密特正交化是朝各个方向做投影的过程，因此并不改变特征向量的特征值。也就是说，可以找到矩阵A的n个正交的特征向量，因此可以将矩阵A对角化，其中Q就是矩阵A的各正交的特征向量组成的矩阵。

created in 2018-08-21 00:00