SVD
矩阵描述的是空间中的线性变换,对于对角矩阵或实对称矩阵($n \times n$)来说,我们总可以找到n个向量,使得矩阵作用在这组向量上仅仅表现为拉伸变换,没有旋转变换。
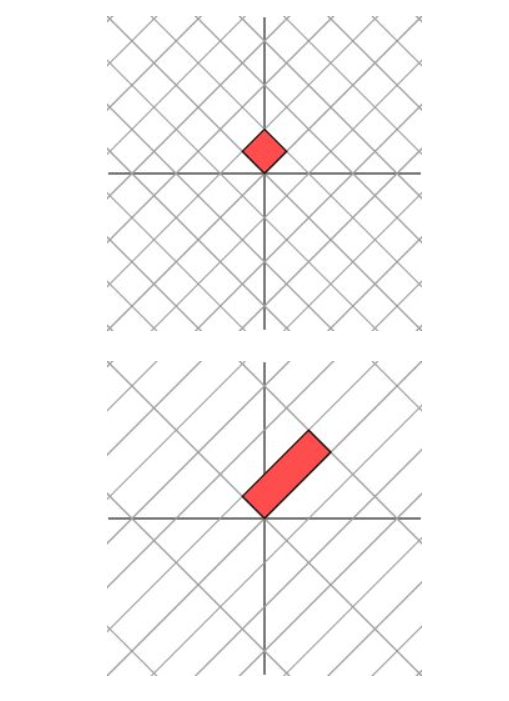
但是对于一般的非对称矩阵,我们再也找不到n个向量,使得矩阵作用之后只有拉伸变换(找不到背后的数学原因是对一般非对称矩阵无法保证在实数域上可对角化)。我们退求其次,找一组向量,使得矩阵作用在该组向量上之后允许有拉伸变换和旋转变换,但要保证变换后的向量依旧互相垂直。这是可以做到的。
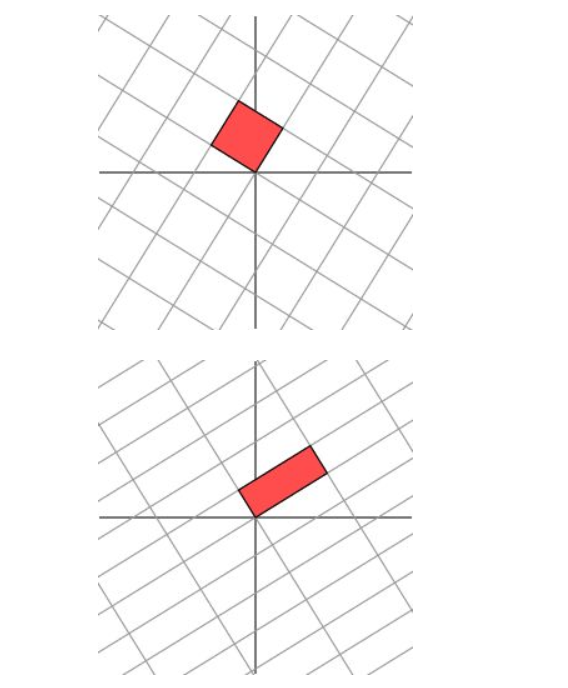
下面我们就可以自然过渡到奇异值分解的引入。奇异值分解的几何含义为:对于任何的一个矩阵,我们要找到一组两两正交单位向量序列,使得矩阵作用在此向量序列上后得到新的向量序列保持两两正交。奇异值的几何含义为:这组变换后的新的向量序列的长度。(特征值分解的几何含义是:对于一个方阵A,要找到n个线性无关的向量,使得矩阵作用在这n个向量上仅仅表现为拉伸变换,没有旋转变换。特征值的几何含义就是拉伸的幅度)
也就是说,对于一般的$m \times n$的矩阵A来说,这个矩阵表示的是一个从n维空间到m维空间的线性变换,而我们找不到一个n维向量x,使得矩阵作用在这组向量上仅仅表现为拉伸变换(因为空间维度发生了改变),即矩阵A没有特征向量。但是,我们可以找到一组n维正交的向量,使得矩阵A作用在这组向量上后得到新的一组m维向量仍然两两正交。
以两个向量为例,当矩阵M(m$\times$n)作用在$\boldsymbol{v}_1$和$\boldsymbol{v}_2$上时,得到$M\boldsymbol{v}_1$和$M\boldsymbol{v}_2$也是正交的。令$u_1$和$u_2$分别是$M\boldsymbol{v}_1$和$M\boldsymbol{v}_2$方向上的单位向量,即$M\boldsymbol{v}_1=\sigma_1u_1,M\boldsymbol{v}_2=\sigma_2u_2$,整理得:
$$
M=M\begin{bmatrix}
v_1 & v_2
\end{bmatrix}\begin{bmatrix}
v_1^T\
v_2^T
\end{bmatrix}=\begin{bmatrix}
\sigma_1u_1 & \sigma_2u_2
\end{bmatrix}\begin{bmatrix}
v_1^T\
v_2^T
\end{bmatrix}=\\
\begin{bmatrix}
u_1 & u_2
\end{bmatrix}\begin{bmatrix}
\sigma_1 & 0\\
0 & \sigma_2
\end{bmatrix}\begin{bmatrix}
v_1^T\
v_2^T
\end{bmatrix}
$$
其中$\boldsymbol{v}_1$和$\boldsymbol{v}_2$是n维向量,$\boldsymbol{u}_1$和$\boldsymbol{u}_2$是m维向量,这样就矩阵M的奇异值分解,奇异值$\sigma_1$和$\sigma_2$分别 是$Mv_1$和$Mv_2$的长度。很容易将结论推广到一般n维情形。