Linear SVM
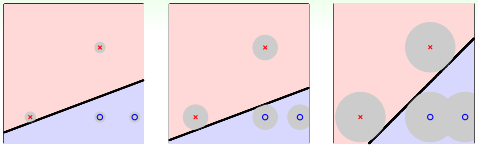
单从分类效果上看,这三条直线都满足要求,而且都满足VC bound要求,模型复杂度$\Omega(H)$是一样的,即具有一定的泛化能力。一般情况下,训练样本外的测试数据应该分布在训练样本附近,但与训练样本的位置有一些偏差,因此,我们不仅希望分界面能将正负样本正确区分,还希望分界面对测试数据的扰动的容忍性要高,也就是要找到一条“最健壮”的线。
如何找到“最健壮”的线?看距离分类线最近的点与分类线的距离,我们把它用margin表示,分类线由权重w决定,目的就是找到使margin最大时对应的w值,即
$$
\begin{align}
&\max \limits_{w}{} &\ \ margin(w) \\
&subject\ to & every\ y_nw^Tx_n>0\\
& &margin(w)=\min \limits_{n=1,\dots,N}{}distance(x_n,w)
\end{align}
$$
$distance(x_n,w)$即点$x_n$到分界面w的距离,$distance(x,b,w)=\frac1{||w||}y_n(w^Tx_n+b)$,那么,目标形式就转换为:
$$
\begin{align}
&\max \limits_{w,b}{} &\ \ margin(w,b) \\
&subject\ to & every\ y_n(w^Tx_n+b)>0\\
& &margin(w,b)=\min \limits_{n=1,\dots,N}{}\frac1{||w||}y_n(w^Tx_n+b)
\end{align}
$$
对上面的式子还不容易求解,我们继续对它进行简化。我们知道分类面$w^Tx+b=0$和$3w^Tx+3b=0$其实是一样的。也就是说,对w和b进行同样的缩放还会得到同一分类面。所以,为了简化计算,我们令距离分类面最近的点满足$y_n(w^Tx_n+b)=1$,那我们所要求的margin就变成了:$margin(b,w)=\frac1{||w||}$,目标形式简化为:
$$
\begin{align}
&\max \limits_{w,b}{} &\ \ \frac1{||w||} \\
&subject\ to &\min \limits_{n=1,\dots,N}{}y_n(w^Tx_n+b)=1
\end{align}
$$
这里省略条件$y_n(w^Tx_n+b)>0$,因为满足条件$y_n(w^Tx_n+b)=1$必然满足大于零的条件。进一步将目标形式做转化:
$$
\begin{align}
&\min \limits_{w,b}{} &\ \ \frac1{2}w^Tw \\
&subject\ to &y_n(w^Tx_n+b)\geq 1\ for\ all\ n
\end{align}
$$
如上图,最小化目标为$\frac1{2}w^Tw$,约束条件为$y_n(w^Tx_n+b)\geq 1$这是一个典型的二次规划问题,即Quadratic Programming(QP)。因为SVM的目标是关于w的二次函数,条件是关于w和b的一次函数,所以,它的求解过程还是比较容易的,可以使用一些软件(例如Matlab)自带的二次规划的库函数来求解。
SVM的这种思想其实与我们之前介绍的机器学习非常重要的正则化regularization思想很类似。regularization的目标是将$E_{in}$最小化,条件是$w^Tw\leq C$;而SVM的目标是$w^Tw$最小化,条件是$y_n(w^Tx_n+b)\geq1$即保证了$E_{in}=0$,就是说regularization与SVM的目标和限制条件分别对调了,其实,考虑的内容是类似的,效果也是相近的。SVM这种方法背后的原理其实就是减少了dichotomies的种类,减少了有效的VC Dimension数量,从而让机器学习的模型具有更好的泛化能力。
注:假设空间H的vc维与数据集D无关,而算法(如Large margin算法)的vc维与数据集有关。
Dual SVM
对于非线性SVM,我们通常可以使用非线性变换将变量从x域转换到z域中。然后,在z域中,根据上一节课的内容,使用线性SVM解决问题即可。
那么,特征转换下,求解QP问题在z域中的维度设为$\hat d +1$,如果维度很大的话,求解这个QP问题也变得很困难。当$\hat d$无限大的时候,问题将会变得难以求解,那么有没有什么办法可以解决这个问题呢?一种方法就是使SVM的求解过程不依赖$\hat d$,即转化为对偶问题。
线性SVM的目标是$min\ \frac12w^Tw$,条件是:$y_n(w^Tz_n+b)\geq 1,\ for\ n=1,2,\cdots,N$。引入拉格朗日因子$\alpha_n$,构造拉格朗日函数:
$$
L(b,w,\alpha)=\frac12w^Tw+\sum_{n=1}^N\alpha_n(1-y_n(w^Tz_n+b))
$$
该函数中包含三个参数:$b,w,\alpha_n$
利用拉格朗日函数,我们可以把SVM的目标及约束转化为下式:
$$
SVM=\min \limits_{b,w}{}(\max \limits_{all\ \alpha_n\geq 0}{}L(b,w,\alpha))
$$
即最小化一个最大化问题,为什么可以这样转换呢?首先我们规定拉格朗日因子$\alpha_n\geq0$,SVM的约束条件为
$(1-y_n(w^Tz_n+b))\leq0$,如果不满足该约束条件,因为$\alpha_n\geq0$,所以$\max \limits_{all\ \alpha_n\geq 0}{}L(b,w,\alpha)$会趋于负无穷;如果满足该约束条件,则当$\sum_n\alpha_n(1-y_n(w^Tz_n+b))=0$时,$L(b,w,\alpha)$有最大值,最大值就是SVM的目标:$\frac12w^Tw$,而$\frac12w^Tw$一定小于无穷,因此我们通过一个最小最大化的转换将SVM的目标及约束条件写在了一个式子中。
将min、max的顺序交换,有
$$
\min \limits_{b,w}{}\max \limits_{all\ \alpha_n\geq 0}{}L(b,w,\alpha)\geq \max \limits_{all\ \alpha_n^{'}\geq 0}{}\min \limits_{b,w}{}L(b,w,\alpha)
$$
已知≥是一种弱对偶关系,在二次规划QP问题中,如果满足以下三个条件:
- 函数是凸的(convex primal)
- 函数有解(feasible primal)
- 条件是线性的(linear constraints)
那么,上述不等式关系就变成强对偶关系,≥变成=,经过推导,SVM对偶问题的解已经转化为无条件形式:
$$
\max \limits_{all\ \alpha_n\geq 0}{}\min \limits_{b,w}{}\frac12w^Tw+\sum_{n=1}^N\alpha_n(1-y_n(w^Tz_n+b))
$$
先看最小化问题$\min \limits_{b,w}{}\frac12w^Tw+\sum_{n=1}^N\alpha_n(1-y_n(w^Tz_n+b))$,根据梯度下降思想:最小值位置满足梯度为0。首先令$L(b,w,\alpha)$对参数b的梯度为零:
$$
\frac{\partial L(b,w,\alpha)}{\partial b}=0=-\sum_{n=1}^N\alpha_ny_n
$$
也就是说,最优解一定满足$\sum_{n=1}^N\alpha_ny_n=0$。把这个条件代入计算max条件中,得到:
$$
\max \limits_{all\ \alpha_n\geq 0}{}\min \limits_{b,w}{}\frac12w^Tw+\sum_{n=1}^N\alpha_n(1-y_n(w^Tz_n))
$$
这样,SVM表达式消去了b,问题化简了一些。然后令$L(b,w,\alpha)$对参数w的梯度为零:
$$
\frac{\partial L(b,w,\alpha)}{\partial w}=0=w-\sum_{n=1}^N\alpha_ny_nz_n
$$
即得到:
$$
w=\sum_{n=1}^N\alpha_ny_nz_n
$$
把这个条件代入并进行化简:

这样,SVM表达式消去了w,问题更加简化了。这时候的条件有3个:
- $\alpha_n\geq0$
- $\sum_{n=1}^N\alpha_ny_n=0 $
- $w=\sum_{n=1}^N\alpha_ny_nz_n$
SVM简化为只有$\alpha_n$的最佳化问题,即计算满足上述三个条件下,函数$-\frac12||\sum_{n=1}^N\alpha_ny_nz_n||^2+\sum_{n=1}^N\alpha_n$最小值时对应的$\alpha_n$是多少。
其中,满足最佳化的条件称之为Karush-Kuhn-Tucker(KKT):

将max问题转化为min问题,再做一些条件整理和推导,得到:

显然,这是一个convex的QP问题,且有N个变量$\alpha_n$,限制条件有N+1个。则根据上一节课讲的QP解法,找到Q,p,A,c对应的值,用软件工具包进行求解即可。
求解过程很清晰,但是值得注意的是,$q_{n,m}=y_ny_mz^T_nz_m$,当N很大的时候,例如N=30000,那么对应的$Q_D$的计算量将会很大,存储空间也很大。所以一般情况下,对dual SVM问题的矩阵$Q_D$,需要使用一些特殊的方法,这部分内容就不再赘述了。
得到$\alpha_n$之后,再根据之前的KKT条件,就可以计算出w和b了。首先利用条件$w=\sum\alpha_ny_nz_n$得到w,然后利用条件$\alpha_n(1-y_n(w^Tz_n+b))=0$,取任一个$\alpha_n≠0$即$\alpha_n>0$的点,得到$1-y_n(w^Tz_n+b)=0$,进而求得$b=y_n-w^Tz_n$。
值得注意的是,计算b值时,任取$\alpha_n>0$的一个点,当$\alpha_n>0$时,有$y_n(w^Tz_n+b)=1$成立,$y_n(w^Tz_n+b)=1$正好表示的是该点是距离分界面最近的点,即支持向量;计算w时,$w=\sum\alpha_ny_nz_n$,只有当$\alpha_n>0$时,才对w有贡献。因此,分类面(w,b)仅由支持向量决定。
也就是说,样本点可以分成两类:一类是support vectors,通过support vectors可以得到分类面;另一类不是support vectors,对我们求得分类面没有影响。
我们来比较一下SVM和PLA的w公式:

我们发现,二者在形式上是相似的。$w_{SVM}$由fattest hyperplane边界上所有的SV决定,$w_{PLA}$由所有当前分类错误的点决定。$w_{SVM}$和$w_{PLA}$都是原始数据点$y_nz_n$的线性组合形式,是原始数据的代表。
总结一下,原始的SVM有$\hat d+1$个参数,$\hat d$为特征维度,有N个限制条件。当$\hat d+1$很大时,求解困难。而Dual Hard_Margin SVM有N个参数,有N+1个限制条件。当数据量N很大时,也同样会增大计算难度。通常情况下,如果特征维度很大而样本数量N不是很大,一般使用Dual SVM来解决问题。
Dual SVM的目的是为了避免计算过程中对$\hat d$的依赖,而只与N有关。但是,Dual SVM是否真的消除了对$\hat d$的依赖呢?其实并没有。因为在计算$q_{n,m}=y_ny_mz_n^Tz_m$的过程中,由z向量引入了$\hat d$,实际上复杂度已经隐藏在计算过程中了。所以,我们的目标并没有实现。

Kernel Trick
我们来看向量$Q_D$中的$q_{n,m}=y_ny_mz_n^Tz_m$,看似这个计算与$\hat d$无关,但是$z_n^Tz_m$的内积中不得不引入$\hat d$。也就是说,如果$\hat d$很大,计算$z_n^Tz_m$的复杂度也会很高,同样会影响QP问题的计算效率。可以说,$q_{n,m}=y_ny_mz_n^Tz_m$这一步是计算的瓶颈所在。
其实问题的关键在于$z_n^Tz_m$内积求解上。我们知道,z是由x经过特征转换而来:
$$z_n^Tz_m=\Phi(x_n)\Phi(x_m)$$
我们先来看一个简单的例子,对于二阶多项式转换,各种排列组合为:

转换之后再做内积并进行推导,得到:
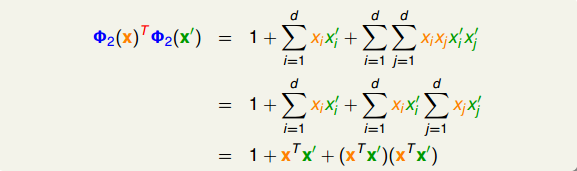
其中$x^Tx'$是x空间中特征向量的内积。所以,$\Phi_2(x)$与$\Phi_2(x')$的内积的复杂度由原来的$O(d^2)$变成$O(d)$,只与x空间的维度d有关,而与z空间的维度$\hat d$无关,这正是我们想要的!
我们把合并特征转换和计算内积这两个步骤的操作叫做Kernel Function,用大写字母K表示。例如刚刚讲的二阶多项式例子,它的kernel function为:
$$
\begin{align}
K_{\Phi}(x,x')&=\Phi(x)^T\Phi(x') \\
K_{\Phi_2}(x,x')&=1+(x^Tx')+(x^Tx')^2
\end{align}
$$
有了kernel function之后,我们来看看它在SVM里面如何使用。在dual SVM中,二次项系数$q_{n,m}$中有z的内积计算,就可以用kernel function替换:
$$q_{n,m}=y_ny_mz_n^Tz_m=y_ny_mK(x_n,x_m)$$
所以,直接计算出$K(x_n,x_m)$,再代入上式,就能得到$q_{n,m}$的值。
$q_{n,m}$值计算之后,就能通过QP得到拉格朗日因子$\alpha_n$。然后,下一步就是计算b(取$\alpha_n$>0的点,即SV),b的表达式中包含z,可以作如下推导:
$$
b=y_s-w^Tz_s=y_s-(\sum_{n=1}^N\alpha_ny_nz_n)^Tz_s=y_s-\sum_{n=1}^N\alpha_ny_n(K(x_n,x_s))
$$
这样得到的b就可以用kernel function表示,而与z空间无关。
最终我们要求的gSVM为:
$$
g_{SVM}(x)=sign(w^T\Phi(x)+b)=sign((\sum_{n=1}^N\alpha_ny_nz_n)^Tz+b)=sign(\sum_{n=1}^N\alpha_ny_n(K(x_n,x))+b)
$$
至此,dual SVM中我们所有需要求解的参数都已经得到了,而且整个计算过程中都没有在z空间作内积,即与z无关。我们把这个过程称为kernel trick,也就是把特征转换和计算内积两个步骤结合起来,用kernel function来避免计算过程中受$\hat d$的影响,从而提高运算速度。我们把这种引入kernel function的SVM称为kernel SVM,它是基于dual SVM推导而来的。kernel SVM同样只用SV($\alpha_n$>0)就能得到最佳分类面,而且整个计算过程中摆脱了$\hat d$的影响,大大提高了计算速度。
多项式核
我们刚刚通过一个特殊的二次多项式导出了相对应的kernel,其实二次多项式的kernel形式是多种的。例如,相应系数的放缩构成完全平方公式等。下面列举了几种常用的二次多项式kernel形式:

比较一下,第一种$\Phi_2(x)$(蓝色标记)和第三种$\Phi_2(x)$(绿色标记)从某种角度来说是一样的,因为都是二次转换,对应到同一个z空间。但是,它们系数不同,内积就会有差异,那么就代表有不同的距离(因为$w=\sum\alpha_ny_nz_n$,因此margin $\frac12w^Tw=\frac12 \sum_{i}\sum_{j}\alpha_i \alpha_j y_iy_jz_i^Tz_j=\frac12 \sum_{i}\sum_{j}\alpha_i \alpha_j y_iy_jK(x_n,x_m)$),最终可能会得到不同的SVM margin。所以,系数不同,可能会得到不同的SVM分界线。通常情况下,第三种$\Phi_2(x)$(绿色标记)简单一些,更加常用。
通过改变不同的系数,得到不同的SVM margin和SV,如何选择正确的kernel,非常重要。
归纳一下,引入ζ≥0和γ>0,对于Q次多项式一般的kernel形式可表示为:

多项式kernel优点:
- 实现数据的线性可分
- 计算过程避免了对$\hat d$的依赖,大大简化了计算量。
- 即使比较高阶的多项式核,分界面也不至于过于复杂,因为SVM的large margin会帮助控制复杂度(自带L2正则项)
高斯核
刚刚我们介绍的Q阶多项式kernel的阶数是有限的,即特征转换的d^是有限的。但是,如果是无限多维的转换Φ(x),是否还能通过kernel的思想,来简化SVM的计算呢?答案是肯定的。
先举个例子,简单起见,假设原空间是一维的,只有一个特征x,我们构造一个kernel function为高斯函数:
$$
K(x,x')=e^{-(x-x')^2}
$$
构造的过程正好与二次多项式kernel的相反,利用反推法,先将上式分解并做泰勒展开:

将构造的K(x,x’)推导展开为两个Φ(x)和Φ(x′)的乘积,其中:
$$
\Phi(x)=e^{-x^2}\cdot (1,\sqrt \frac{2}{1!}x,\sqrt \frac{2^2}{2!}x^2,\cdots)
$$
通过反推,我们得到了Φ(x),Φ(x)是无限多维的,它就可以当成特征转换的函数,且d^是无限的。这种Φ(x)得到的核函数即为Gaussian kernel。引入缩放因子γ>0,它对应的Gaussian kernel表达式为:
$$
K(x,x')=e^{-\gamma||x-x'||^2}
$$
那么引入了高斯核函数,将有限维度的特征转换拓展到无限的特征转换中。根据本节课上一小节的内容,由K,计算得到αn和b,进而得到矩gSVM。将其中的核函数K用高斯核函数代替,得到:
$$
g_{SVM}(x)=sign(\sum_{SV}\alpha_ny_nK(x_n,x)+b)=sign(\sum_{SV}\alpha_ny_ne^{(-\gamma||x-x_n||^2)}+b)
$$
通过上式可以看出,gSVM有n个高斯函数线性组合而成,其中n是SV的个数。而且,每个高斯函数的中心都是对应的SV。通常我们也把高斯核函数称为径向基函数(Radial Basis Function, RBF)。
总结一下,kernel SVM可以获得large-margin的hyperplanes,并且可以通过高阶的特征转换使Ein尽可能地小。kernel的引入大大简化了dual SVM的计算量。而且,Gaussian kernel能将特征转换扩展到无限维,并使用有限个SV数量的高斯函数构造出矩gSVM。
值得注意的是,缩放因子γ取值不同,会得到不同的高斯核函数,hyperplanes不同,分类效果也有很大的差异。举个例子,γ分别取1, 10, 100时对应的分类效果如下:
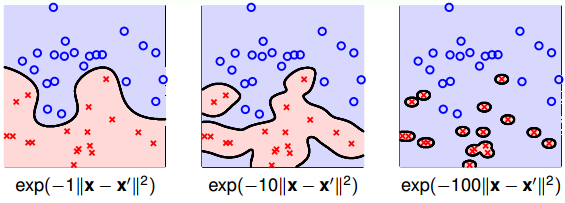
从图中可以看出,当γ比较小的时候,分类线比较光滑,当γ越来越大的时候,分类线变得越来越复杂和扭曲,直到最后,分类线变成一个个独立的小区域,像小岛一样将每个样本单独包起来了。为什么会出现这种区别呢?这是因为γ越大,其对应的高斯核函数越尖瘦,那么有限个高斯核函数的线性组合就比较离散,分类效果并不好。所以,SVM也会出现过拟合现象,γ的正确选择尤为重要,不能太大。
Comparison of Kernels
- Linear Kernel的优点是计算简单、快速,可以直接使用QP快速得到参数值,而且从视觉上分类效果非常直观,便于理解;缺点是如果数据不是线性可分的情况,Linear Kernel就不能使用了。
- Polynomial Kernel的优点是阶数Q可以灵活设置,相比linear kernel限制更少,更贴近实际样本分布;缺点是当Q很大时,K的数值范围波动很大,而且参数个数较多,难以选择合适的值。
- Gaussian Kernel的优点是边界更加复杂多样,能最准确地区分数据样本,数值计算K值波动较小,而且只有一个参数,容易选择;缺点是由于特征转换到无限维度中,w没有求解出来,计算速度要低于linear kernel,而且可能会发生过拟合。
除了这三种kernel之外,我们还可以使用其它形式的kernel。首先,我们考虑kernel是什么?实际上kernel代表的是两笔资料x和x’,特征变换后的相似性即内积。但是不能说任何计算相似性的函数都可以是kernel。有效的kernel还需满足几个条件:
- K是对称的
- K是半正定的
Soft-Margin Support Vector Machine
Kernel SVM将特征转换和计算内积这两个步骤合并起来,简化计算、提高计算速度,再用Dual SVM的求解方法来解决。Kernel SVM不仅能解决简单的线性分类问题,也可以求解非常复杂甚至是无限多维的分类问题,关键在于核函数的选择,例如线性核函数、多项式核函数和高斯核函数等等。但是,我们之前讲的这些方法都是Hard-Margin SVM,即必须将所有的样本都分类正确才行。这往往需要更多更复杂的特征转换,甚至造成过拟合。本节课将介绍一种Soft-Margin SVM,目的是让分类错误的点越少越好,而不是必须将所有点分类正确,也就是允许有noise存在。这种做法很大程度上不会使模型过于复杂,不会造成过拟合,而且分类效果是令人满意的。
SVM同样可能会造成overfit。原因就是我们坚持要将所有的样本都分类正确,即不允许错误存在,因此我们使用了复杂的特征转换,导致模型过于复杂。
如下图所示,左边的图Φ1是线性的,虽然有几个点分类错误,但是大部分都能完全分开。右边的图Φ4是四次多项式,所有点都分类正确了,但是模型比较复杂,可能造成过拟合。直观上来说,左边的图是更合理的模型。

如何避免过拟合?方法是允许有分类错误的点,即把某些点当作是noise,放弃这些noise点,但是尽量让这些noise个数越少越好。回顾一下我们在机器学习基石笔记中介绍的pocket算法,pocket的思想不是将所有点完全分开,而是找到一条分类线能让分类错误的点最少。而Hard-Margin SVM的目标是将所有点都完全分开,不允许有错误点存在。为了防止过拟合,我们可以借鉴pocket的思想,即允许有犯错误的点,目标是让这些点越少越好。
为了引入允许犯错误的点,我们将Hard-Margin SVM的目标和条件做一些结合和修正,转换为如下形式:
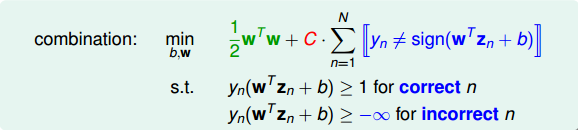
修正后的条件中,对于分类正确的点,仍需满足$y_n(w^Tz_n+b)\geq 1$,而对于noise点,满足$y_n(w^Tz_n+b)\geq -\infty$,即没有限制。修正后的目标除了$\frac12w^Tw$项,还添加了$y_n\neq sign(w^Tz_n+b)$,即noise点的个数。参数C的引入是为了权衡目标第一项和第二项的关系,即权衡large margin和noise tolerance的关系。
我们再对上述的条件做修正,将两个条件合并,得到:
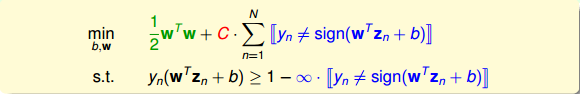
这个式子存在两个不足的地方。首先,最小化目标中第二项是非线性的,不满足QP的条件,所以无法使用dual或者kernel SVM来计算。然后,对于犯错误的点,有的离边界很近,即error小,而有的离边界很远,error很大,上式的条件和目标没有区分small error和large error。这种分类效果是不完美的。
为了改正这些不足,我们继续做如下修正:

修正后的表达式中,我们引入了新的参数ξn来表示每个点犯错误的程度值,ξn≥0。通过使用error值的大小代替是否有error,让问题变得易于求解,满足QP形式要求。这种方法类似于我们在机器学习基石笔记中介绍的0/1 error和squared error。这种soft-margin SVM引入新的参数ξ。
至此,最终的Soft-Margin SVM的目标为:
$$
min(b,w,\xi)\ \frac12w^Tw+C\cdot\sum_{n=1}^N\xi_n
$$
条件是:
$$
\begin{align}
y_n(w^Tz_n+b)&\geq 1-\xi_n \\
&\xi_n\geq0
\end{align}
$$
其中,ξn表示每个点犯错误的程度,ξn=0,表示没有错误,ξn越大,表示错误越大,即点距离边界(负的)越大。参数C表示尽可能选择宽边界和尽可能不要犯错两者之间的权衡,因为边界宽了,往往犯错误的点会增加。large C表示希望得到更少的分类错误,即不惜选择窄边界也要尽可能把更多点正确分类;small C表示希望得到更宽的边界,即不惜增加错误点个数也要选择更宽的分类边界。
与之对应的QP问题中,由于新的参数ξn的引入,总共参数个数为$\hat d+1+N$,限制条件添加了ξn≥0,则总条件个数为2N。
Dual Problem
接下来,我们将推导Soft-Margin SVM的对偶dual形式,从而让QP计算更加简单,并便于引入kernel算法。首先,我们把Soft-Margin SVM的原始形式写出来:
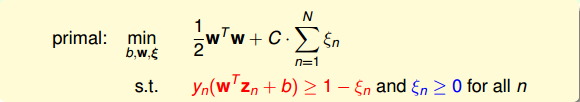
然后,跟我们在第二节课中介绍的Hard-Margin SVM做法一样,构造一个拉格朗日函数。因为引入了ξn,原始问题有两类条件,所以包含了两个拉格朗日因子αn和βn。拉格朗日函数可表示为如下形式:
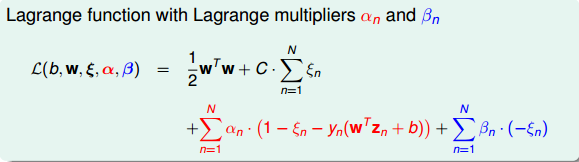
接下来,我们跟第二节课中的做法一样,利用Lagrange dual problem,将Soft-Margin SVM问题转换为如下形式:
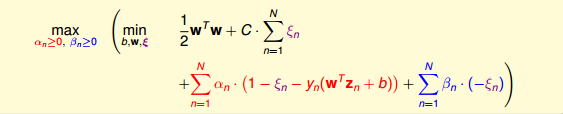
根据之前介绍的KKT条件,我们对上式进行简化。上式括号里面的是对拉格朗日函数L(b,w,ξ,α,β)计算最小值。那么根据梯度下降算法思想:最小值位置满足梯度为零。
我们先对ξn做偏微分:
$$
\frac{\partial L}{\partial \xi_n}=0=C-\alpha_n-\beta_n
$$
根据上式,得到$\beta_n=C-\alpha_n$,因为有βn≥0,所以限制$0\leq\alpha_n\leq C$。将βn=C−αn代入到dual形式中并化简,我们发现βn和ξn都被消去了:
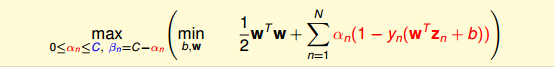
这个形式跟Hard-Margin SVM中的dual形式是基本一致的,只是条件不同。那么,我们分别令拉个朗日函数L对b和w的偏导数为零,分别得到:
$$
\begin{align}
&\sum_{n=1}^N\alpha_ny_n=0 \\
&w=\sum_{n=1}^N\alpha_ny_nz_n
\end{align}
$$
经过化简和推导,最终标准的Soft-Margin SVM的Dual形式如下图所示:
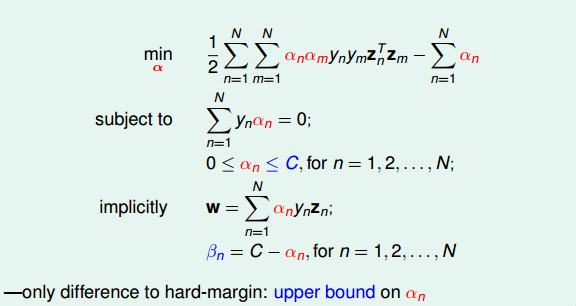
Soft-Margin SVM Dual与Hard-Margin SVM Dual基本一致,只有一些条件不同。Hard-Margin SVM Dual中αn≥0,而Soft-Margin SVM Dual中0≤αn≤C,且新的拉格朗日因子βn=C−αn。在QP问题中,Soft-Margin SVM Dual的参数αn同样是N个,但是,条件由Hard-Margin SVM Dual中的N+1个变成2N+1个,这是因为多了N个αn的上界条件。
推导完Soft-Margin SVM Dual的简化形式后,就可以利用QP,找到Q,p,A,c对应的值,用软件工具包得到αn的值。或者利用核函数的方式,同样可以简化计算,优化分类效果。Soft-Margin SVM Dual计算αn的方法过程与Hard-Margin SVM Dual的过程是相同的。
但是如何根据αn的值计算b呢?在Hard-Margin SVM Dual中,有complementary slackness条件:$\alpha_n(1-y_n(w^Tz_n+b))=0$,找到SV,即αs>0的点,计算得到$b=y_s-w^Tz_s$。
那么,在Soft-Margin SVM Dual中,相应的complementary slackness条件有两个(因为两个拉格朗日因子αn和βn):
$$
\begin{align}
&\alpha_n(1-\xi_n-y_n(w^Tz_n+b))=0 \\
&\beta_n\xi_n=(C-\alpha_n)\xi=0
\end{align}
$$
找到SV,即αs>0的点,由于参数ξn的存在,还不能完全计算出b的值。根据第二个complementary slackness条件,如果令C−αn≠0,即αn≠C,则一定有ξn=0,代入到第一个complementary slackness条件,即可计算得到$b=y_s-w^Tz_s$。我们把$0<\alpha_s
从上图可以看出,C=1时,margin比较粗,但是分类错误的点也比较多,当C越来越大的时候,margin越来越细,分类错误的点也在减少。正如前面介绍的,C值反映了margin和分类正确的一个权衡。C越小,越倾向于得到粗的margin,宁可增加分类错误的点;C越大,越倾向于得到高的分类正确率,宁可margin很细。我们发现,当C值很大的时候,虽然分类正确率提高,但很可能把noise也进行了处理,从而可能造成过拟合。也就是说Soft-Margin Gaussian SVM同样可能会出现过拟合现象,所以参数(γ,C)的选择非常重要。
我们再来看看αn取不同值是对应的物理意义。已知0≤αn≤C满足两个complementary slackness条件:
$$
\begin{align}
\alpha_n(1- &\xi_n-y_n(w^Tz_n+b))=0 \\
\beta_n\xi_n&=(C-\alpha_n)\xi=0
\end{align}
$$
若αn=0,得ξn=0。ξn=0表示该点没有犯错,αn=0表示该点不是SV。所以对应的点在margin之外(或者在margin上),且均分类正确。
若0<αn<C,得ξn=0,且yn(wTzn+b)=1。ξn=0表示该点没有犯错,yn(wTzn+b)=1表示该点在margin上。这些点即free SV,确定了b的值。
若αn=C,不能确定ξn是否为零,且得到1−yn(wTzn+b)=ξn,这个式表示该点偏离margin的程度,ξn越大,偏离margin的程度越大。只有当ξn=0时,该点落在margin上。所以这种情况对应的点在margin之内负方向(或者在margin上),有分类正确也有分类错误的。这些点称为bounded SV。
所以,在Soft-Margin SVM Dual中,根据αn的取值,就可以推断数据点在空间的分布情况。
总结一下,Soft-Margin SVM的出发点与Hard-Margin SVM不同,不一定要将所有的样本点都完全分开,允许有分类错误的点,而使margin比较宽。然后,我们增加了ξn作为分类错误的惩罚项,根据之前介绍的Dual SVM,推导出了Soft-Margin SVM的QP形式。得到的αn除了要满足大于零,还有一个上界C。接着介绍了通过αn值的大小,可以将数据点分为三种:non-SVs,free SVs,bounded SVs,这种更清晰的物理解释便于数据分析。最后介绍了如何选择合适的SVM模型,通常的办法是cross-validation和利用SV的数量进行筛选。