Motivation of Boosting
我们先来看一个简单的识别苹果的例子,老师展示20张图片,让6岁孩子们通过观察,判断其中哪些图片的内容是苹果。从判断的过程中推导如何解决二元分类问题的方法。
显然这是一个监督式学习,20张图片包括它的标签都是已知的。首先,学生Michael回答说:所有的苹果应该是圆形的。根据Michael的判断,对应到20张图片中去,大部分苹果能被识别出来,但也有错误。其中错误包括有的苹果不是圆形,而且圆形的水果也不一定是苹果。如下图所示:

上图中蓝色区域的图片代表分类错误。显然,只用“苹果是圆形的”这一个条件不能保证分类效果很好。我们把蓝色区域(分类错误的图片)放大,分类正确的图片缩小,这样在接下来的分类中就会更加注重这些错误样本。然后,学生Tina观察被放大的错误样本和上一轮被缩小的正确样本,回答说:苹果应该是红色的。根据Tina的判断,得到的结果如下图所示:

上图中蓝色区域的图片一样代表分类错误,即根据这个苹果是红色的条件,使得青苹果和草莓、西红柿都出现了判断错误。那么结果就是把这些分类错误的样本放大化,其它正确的样本缩小化。同样,这样在接下来的分类中就会更加注重这些错误样本。接着,学生Joey经过观察又说:苹果也可能是绿色的。根据Joey的判断,得到的结果如下图所示:

上图中蓝色区域的图片一样代表分类错误,根据苹果是绿色的条件,使得图中蓝色区域都出现了判断错误。同样把这些分类错误的样本放大化,其它正确的样本缩小化,在下一轮判断继续对其修正。后来,学生Jessica又发现:上面有梗的才是苹果。得到如下结果:

经过这几个同学的推论,苹果被定义为:圆的,红色的,也可能是绿色的,上面有梗。从一个一个的推导过程中,我们似乎得到一个较为准确的苹果的定义。虽然可能不是非常准确,但是要比单一的条件要好得多。也就是说把所有学生对苹果的定义融合起来,最终得到一个比较好的对苹果的总体定义。这种做法就是我们本节课将要讨论的演算法。这些学生代表的就是简单的hypothses $g_{t}$,将所有$g_{t}$融合,得到很好的预测模型$G$。例如,二维平面上简单的hypotheses(水平线和垂直线),这些简单的$g_{t}$最终组成的较复杂的分类线能够较好地将正负样本完全分开,即得到了好的预测模型。
所以,上个苹果的例子中,不同的学生代表不同的hypotheses $g_{t}$;最终得到的苹果总体定义就代表hypotheses $G$;而老师就代表演算法$A$,指导学生的注意力集中到关键的例子中(错误样本),从而得到更好的苹果定义。其中的数学原理,我们下一部分详细介绍。
Diversity by Re-weighting
在介绍这个演算法之前,我们先来讲一下上节课就介绍过的bagging。bagging的核心是bootstrapping,通过对原始数据集$D$不断进行bootstrap的抽样动作,得到与$D$类似的数据集$D_{t}$,每组$D_{t}$都能得到相应的$g_{t}$,从而进行aggregation的操作。现在,假如包含四个样本的$D$经过bootstrap,得到新的$D_{t}$如下:
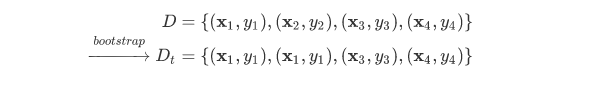
可以看出$D_{t}$完全是$D$经过bootstrap得到的,其中样本$ (\mathbf{x}_1,y_{1})$出现2次,$ (\mathbf{x}_2,y_{2})$出现1次,$ (\mathbf{x}_3,y_{3})$出现0次,$ (\mathbf{x}_4,y_{4})$出现1次。那么,对于新的$D_{t}$,把它交给base algorithm,找出$E_{in}$最小时对应的$g_{t}$,如(1)式所示。
$$
E_{in}^{0/1}(h)=\frac{1}{4}\sum_{(\mathbf{x},y)\epsilon D_{t}}^{e}\left [ y\neq h(\mathbf{x}) \right ]
$$
引入一个参数$u_{i}$来表示原$D$中第i个样本在$D_{t}$中出现的次数,那么(1)式可以写成
$$
E_{in}^{u}(h)=\frac{1}{4}\sum_{n=1}^{4}u_{n}^{(t)}\left [ y\neq h(\mathbf{x}) \right ]
$$
参数$u_{i}$相当于是权重因子,当$D_{t}$中第i个样本出现的次数越多的时候,那么对应的uiui越大,表示在error function中对该样本的惩罚越多。所以,从另外一个角度来看bagging,它其实就是通过bootstrap的方式,来得到这些$u_{i}$值,作为样本的权重因子,再用base algorithm最小化包含$u_{i}$的error function,得到不同的$g_{t}$。这个error function被称为bootstrap-weighted error,这种算法叫做Weightd Base Algorithm,目的就是最小化bootstrap-weighted error。
$$
min\ \ E_{in}^{u}(h)=\frac{1}{4}\sum_{n=1}^{4}u_{n}\cdot err(y_{n},h(\mathbf{x}_{n}))
$$
其实,这种带有权重的样本很容易适配之前学习过的模型中(之前学过的模型默认样本均为1,即样本权重相等),如SVM,LR。例如在soft-margin SVM中…………(待续)。又例如在采用SGD的LR中,随机选取某个样本点计算梯度,那么在选取的时候,权重高的样本被选取的概率大于权重低的样本即可,这样,LR便可以支持带权重的样本了。
知道了$u_{i}$的概念后,我们知道不同的$u_{i}$组合经过base algorithm得到不同的$g_{t}$。那么如何选取$u_{i}$,使得到的$g_{t}$之间有很大的不同呢?之所以要让所有的$g_{t}$差别很大,是因为上节课aggregation中,我们介绍过$g_{t}$越不一样,其aggregation的效果越好,即每个人的意见越不相同,越能运用集体的智慧,得到好的预测模型,好而不同嘛。
为了得到不同的$g_{t}$,我们先来看看$g_{t}$和$g_{t+1}$是怎么得到的:
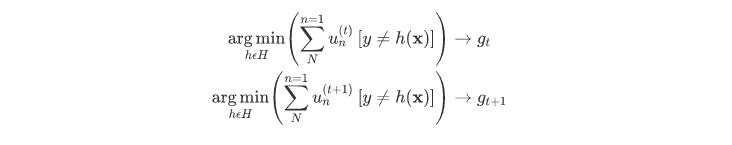
如上所示,$g_{t}$是由$u^{t}$最小化$E_{in}(h)$到的,$g_{t+1}$是由$u_{n}^{t+1}$最小化$E_{in}(h)$得到的。如果$g_{t}$这个模型在使用$u_{n}^{t+1}$的时候得到的$E_{in}(h)$最大,那就表示由$u^{t+1}$计算的$g_{t+1}$会与$g_{t}$有很大不同,而这正是我们希望看到的。怎么做呢?如果在$g_{t}$作用下,$u_{n}^{t+1}$中的表现(即error)近似为0.5的时候,表明$g_{t}$对$u_{n}^{t+1}$的预测分类没有什么作用,就像抛硬币一样,是随机选择的,其数学表达式如下所示:
$$
\begin{align}
idea: construct \ u^{t+1} \ to\ make\ g_{t}\ randomlike:\
\
\frac{\sum_{n=1}^{N}u_{n}^{t+1}\left [ y\neq h(\mathbf{x}) \right ] }{\sum_{n=1}^{N}u_{n}^{t+1}}
\end{align}
$$
乍看上面这个式子,似乎不好求解。但是,我们对它做一些等价处理,其中分式中分子可以看成$g_{t}$作用下犯错误的点,而分母可以看成犯错的点和没有犯错误的点的集合,即所有样本点。其中犯错误的点和没有犯错误的点分别用橘色方块和绿色圆圈表示:
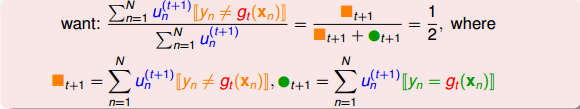
要让分式等于0.5,显然只要将犯错误的点和没有犯错误的点的数量调成一样就可以了。也就是说,在$g_{t}$作用下,将所有犯错的点的权重$u_{n}^{(t+1)}$之和等于所有没有犯错的点的权重$u_{n}^{(t+1)}$之和。一种简单的方法就是利用放大和缩小的思想(本节课开始引入识别苹果的例子中提到的放大图片和缩小图片就是这个目的),将错误分类点的$u_{n}^{(t)}$和没有犯错误的$u_{n}^{(t)}$做相应的乘积操作,使得二者值变成相等。例如所有误分类点的权重和为1126,所有正确分类点的权重和为6211,要让误分类比例正好是0.5,可以这样做,
对于$g_{t}$作用下犯错误的点:
$$
u_{n}^{t+1}\leftarrow u_{n}^{t}\cdot 6211
$$
对于$g_{t}$作用下正确分类的点:
$$
u_{n}^{t+1}\leftarrow u_{n}^{t}\cdot 1126
$$
或者利用犯错的比例来做,即令weighted incorrect rate和weighted correct rate分别设为$u_{n}^{t+1}\leftarrow u_{n}^{t}\cdot \frac{6211}{7737}$和$u_{n}^{t+1}\leftarrow u_{n}^{t}\cdot \frac{1126}{7737}$,设加权分类误差率为$\epsilon _{t}$
对于$g_{t}$作用下犯错误的点:
$$
u_{n}^{t+1}\leftarrow u_{n}^{t}\cdot (1-\epsilon_{t})
$$
对于$g_{t}$作用下正确分类的点:
$$
u_{n}^{t+1}\leftarrow u_{n}^{t}\cdot\epsilon_{t}
$$
Adaptive Boosting Algorithm
上一部分,我们介绍了在计算$u_{n}^{t+1}$的时候,$u_{n}^{t}$分别乘以$1-\epsilon_{t}$和$\epsilon_{t}$。下面将构造一个新的尺度因子:
$$
\lozenge t=\sqrt{\frac{1-\epsilon_{t}}{\epsilon_{t}}}
$$
那么引入这个新的尺度因子之后,对于错误点的$u_{n}^{t}$,将它乘以$\lozenge t$;对于正确的$u_{n}^{t}$,将它除以$\lozenge t$,这种操作跟之前介绍的分别乘以$1-\epsilon_{t}$和$\epsilon_{t}$的效果是一样的。之所以引入$\lozenge t$是因为它告诉我们更多的物理意义。因为如果$\epsilon_{t}<0.5$,那么$\lozenge t\geq 1$,那么接下来错误点的$u_{n}^{t}$与$\lozenge t$的乘积就相当于把错误点放大了,而正确点的$u_{n}^{t}$与$\lozenge t$的相除就相当于把正确点缩小了。这种scale up incorrect和scale down correct的做法与本节课开始介绍的学生识别苹果的例子中放大错误的图片和缩小正确的图片是一个原理,让学生能够将注意力更多地放在犯错误的点上。通过这种scaling-up incorrect的操作,能够保证得到不同于$g_{t}$的$g_{t+1}$。
从这个概念出发,我们可以得到一个初步的演算法,具体迭代步骤如下:

但是,上述步骤还有两个问题没有解决,第一个问题是初始的$u_{n}^{1}$应为多少呢?一般来说,设$u_{n}^{1}=\frac{1}{N}$即可,这样最开始的$g_{1}$就能由此推导。第二个问题,最终的$G(x)$应该怎么求?是将所有的$g_{t}$合并uniform在一起吗?一般来说并不是这样直接uniform求解,因为是$g_{t+1}$通过$g_{t}$得来的,二者在$E_{in}$上的表现差别比较大。所以,一般是对所有的$g_{t}$进行linear或者non-linear组合来得到$G(x)$。
那么如何将所有的$g_{t}$进行linear组合呢?方法是计算$g_{t}$的同时,就能计算得到其线性组合系数$\alpha_{t}$,即aggregate linearly on the fly。这种算法使最终求得$g_{t+1}$的时候,所有$g_{t}$的线性组合系数$\alpha_{t}$也求得了,不用再重新计算$\alpha_{t}$了。这种Linear Aggregation on the Fly算法流程为:

线性组合系数$\alpha_{t}$是如何确定的呢?从直观上看,如果某个$g_{t}$对应的$\epsilon_{t}$很小,说明其分类效果好,那么其在最后的$G(x)$中的系数$\alpha_{t}$应该较大,即:$\epsilon_{t}$越小,对应的$\alpha_{t}$应该越大,反之亦然。又因为$\epsilon_{t}$越小,$\lozenge t$越大,因此$\alpha_{t}$ 和$\lozenge t$是正相关的,我们构造$\alpha_{t}$为:
$$
\alpha_{t}=ln(\lozenge t)
$$
$\alpha_{t}$这样取值是有物理意义的,例如当$\epsilon_{t}=0.5$时,error很大,跟掷骰子这样的随机过程没什么两样,此时对应的$\lozenge t=1$,$\alpha_{t}=0$,即此$g_{t}$对$G(x)$没有什么贡献。而当$\epsilon_{t}=0$时,没有error,表示该$g_{t}$预测非常准,此时对应的$\lozenge t=\infty$,$\alpha_{t}=\infty$,即此$g_{t}$对$G(x)$贡献非常大。
这种算法被称为Adaptive Boosting。它由三部分构成:base learning algorithm A,re-weighting factor $\lozenge t$和linear aggregation $\alpha _{t}$。这三部分分别对应于我们在本节课开始介绍的例子中的Student,Teacher和Class。
综上所述,完整的adaptive boosting(AdaBoost)Algorithm流程如下:

从我们之前介绍过的VC bound角度来看,AdaBoost算法理论上满足:

上式中,$E_{out}(G)$的上界由两部分组成,一项是$E_{in}(G)$,另一项是模型复杂度O(*)。模型复杂度中$d_{vc}(H)$是$g_{t}$的VC Dimension,T是迭代次数,可以证明$d_{vc}(H)$服从$O(d_{vc}(H)⋅Tlog T)$。对这个VC bound中的第一项$E_{in}(G)$来说,有一个很好的性质:如果满足$\epsilon_{t}\leq \epsilon <0.5$,则经过$T=O(log N)$次迭代之后,$E_{in}(G)$能减小到等于零的程度。而当$N$很大的时候,其中第二项也能变得很小。因为这两项都能变得很小,那么整个$E_{out}(G)$就能被限定在一个有限的上界中。其实,这种性质也正是AdaBoost算法的精髓所在。只要每次的$\epsilon_{t}\leq \epsilon <0.5$,即所选择的$g_{t}$比乱猜的表现好一点点,那么经过每次迭代之后,$g_{t}$的表现都会比原来更好一些,逐渐变强,最终得到$E_{in}(G)=0$且$E_{out}(G)$很小。
Adaptive Boosting in Action
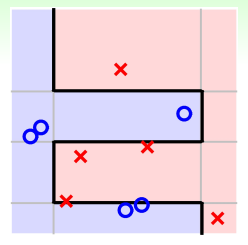
下面介绍一个例子,来看看AdaBoost是如何使用decision stump解决实际问题的。如下图所示,二维平面上分布一些正负样本点,利用decision stump来做切割。
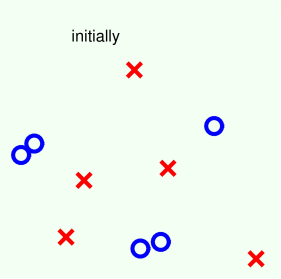
第一步:
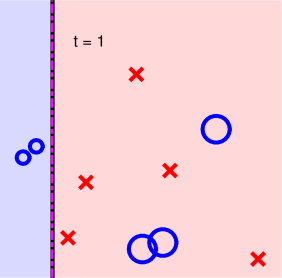
第二步:
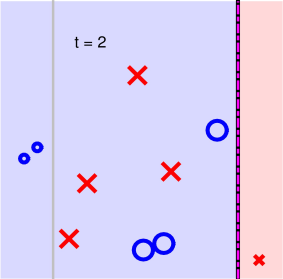
第三步:
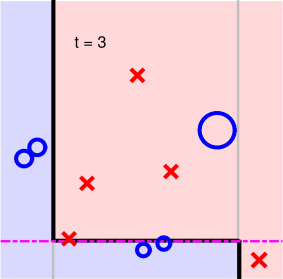
第四步:
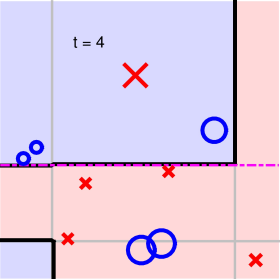
第五步:
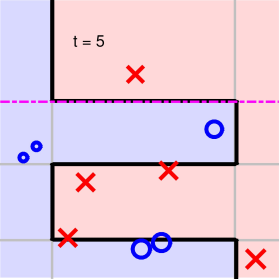
可以看出,AdaBoost-Stump这种非线性模型得到的分界线对正负样本有较好的分离效果。
总结
本节课主要介绍了Adaptive Boosting。首先通过讲一个老师教小学生识别苹果的例子,来引入Boosting的思想,即把许多“弱弱”的hypotheses合并起来,变成很强的预测模型。然后重点介绍这种算法如何实现,关键在于每次迭代时,给予样本不同的系数$u_{n}^{t}$,宗旨是放大错误样本,缩小正确样本,得到不同的小g。并且在每次迭代时根据错误$\epsilon$值的大小,给予不同$g_{t}$不同的权重。最终由不同的$g_{t}$进行组合得到整体的预测模型G。实际证明,Adaptive Boosting能够得到有效的预测模型。
个人总结
原理理解
- AdaBoost是利用前一轮迭代的误差率来更新训练集的权重,减小上一轮被正确分类的样本权值,提高那些被错误分类的样本权值。然后,再根据所采用的一些基本机器学习算法进行学习,比如逻辑回归。
- AdaBoost采用加权多数表决的方法,加大分类误差率小的弱分类器的权重,减小分类误差率大的弱分类器的权重。即正确率高分得好的弱分类器在强分类器中有较大的发言权。
算法流程
输入:数据集$D$
输出:强分类器
-
初始化样本权重$u_{}^{(1)}=(w_{1,1},w_{1,2},...,w_{1,i}),w_{1,i}=\frac{1}{N},i=1,2,...N$
-
对于$t=1,2,...,T$
(1). 使用具有权值分布$u_{}^{(t)}$的训练集进行训练,得到弱分类器$g_t(x)$
(2). 计算$g_t(x)$在训练数据集上的分类误差率:
$$
e_t=\sum_{i=1}^{N}w_{t,i}I(g_t(x_i)\neq y_i)
$$
(3). 计算$g_t(x)$在强分类器中所占的权重:
$$
\alpha_t=\frac{1}{2}log\frac{1-e_t}{e_t}
$$
(4). 更新训练数据集的样本权重分布($z_t$是归一化因子)
$$
w_{t+1,i}=\frac{w_{t,i}}{z_t}exp(-\alpha_ty_ig_t(x_i)),i=1,2,...,N
$$
$$
z_t=\sum_{i=1}^{N}w_{t,i}exp(-\alpha_ty_ig_t(x_i))
$$
- 将所有的$g_t$组合得到最终的分类器
$$
G(x)=sign(\sum_{t=1}^{T}\alpha_tg_t(x))
$$
公式推导
现在来推导上述公式是怎么来的,推导的前提是adaboost用于解决二分类问题,且
$$y_i \in \{1,-1\}$$
假设已经经过t-1轮迭代,得到$G_{t-1}(x)$,由于采用加法模型,那么第t轮迭代得到$\alpha_t,g_t,G_{t}(x)$,其中
$$
G_{t}(x)=G_{t-1}(x)+\alpha_tg_t(x)
$$
AdaBoost是采用指数损失,损失函数为
$$
Loss=\sum_{i=1}^{N}exp(-y_iG_t(x_i))=\sum_{i=1}^{N}exp(-y_i(G_{t-1}(x_i)+\alpha_tg_t(x_i)))
$$
上式可以写成
$$
Loss=\sum_{i=1}^{N}\bar{w}_{t,i}exp(-y_i\alpha_tg_t(x_i))
$$
其中,$\bar{w}_{t,i}=exp(-y_iG_{t-1}(x_i))$,因为$\bar{w}_{t,i}$既不依赖$\alpha_t$,也不依赖$g_t$,所以与最小化无关,但$\bar{w}_{t,i}$依赖于$G_{t-1}(x)$,随着每一轮迭代而发生改变。
现在要求使$Loss$最小的$\alpha_t,g_t$,先求$g_t(x)$,对任意$\alpha>0$,使Loss最小的$g_t(x)$可由下式得到
$$
g_t(x)=\mathop{\arg\min}_{g}\sum_{i=1}^{N}\bar{w}_{t,i}I(y_i \neq g(x_i))
$$
此分类器$g_t(x)$即为adaboost第t轮的基分类器,因为它是使第t轮加权训练数据分类误差率最小的基分类器。
第二步求$\alpha_t$,继续化简Loss
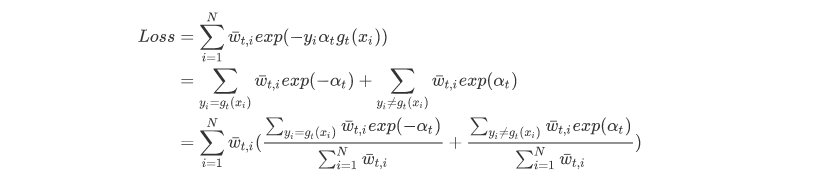
仔细一看,$\frac{\sum_{y_i\neq g_t(x_i)}\bar{w}_{t,i}}{\sum_{i=1}^{N}\bar{w}_{t,i}}$不就是第t轮的加权分类误差率嘛,记为$e_t$,那么Loss可以写为
$$
Loss=\sum_{i=1}^{N}\bar{w}_{t,i}((1-e_t)\cdot exp(-\alpha_t)+e_t\cdot exp(\alpha_t))
$$
对$\alpha_t$求导,令$\frac{\partial Loss }{\partial \alpha_t}=0$,得到
$$
\alpha_t=\frac{1}{2}log\frac{1-e_t}{e_t}
$$
由$G_{t}(x)=G_{t-1}(x)+\alpha_tg_t(x)$以及 $\bar{w}_{t,i}=exp(-y_iG_{t-1}(x_i))$可得
$$
\bar{w}_{t+1,i}=\bar{w}_{t,i}exp(-y_i\alpha_tg_t(x_i))
$$
参考
李航 统计学习方法