Gradient Boosted Decision Tree - zhanghongwei's personal knowledge wiki

Table of Contents

Adaboost + decision tree
从优化的角度来看Adaboost
Gradient Boosting
Summary of Aggregation Models
总结
思考
个人总结
参考

Adaboost + decision tree

考虑将Adaboost和decision tree 结合起来的算法为：

在每轮decision tree的学习中，利用带权重$u^{(t)}$的样本集$D$训练得到最好的$g_t$；最后得出每个$g_t$所占的权重，线性组合得到$G$。

但是在AdaBoost-DTree中需要注意的一点是每个样本的权重$u^{(t)}$。但是在决策树模型中，例如C&RT算法中并没有引入$u^{(t)}$。那么，如何在决策树中引入这些权重$u^{(t)}$来得到不同的$g_t$而又不改变原来的决策树算法呢？

在Adaptive Boosting中，我们使用了weighted algorithm，形如：
$$
E_{in}^u(h)=\frac{1}{N}\sum_{n=1}^{N}u_n\cdot err(y_n,h(x_n))
$$
每个犯错误的样本点乘以相应的权重，求和再平均，最终得到了$E_{in}^u(h)$。如果在决策树中使用这种方法，将当前分支下犯错误的点赋予权重，每层分支都这样做，会比较复杂，不易求解。为了简化运算，保持决策树算法本身的稳定性和封闭性，我们可以把决策树算法当成一个黑盒子，即不改变其结构，不对算法本身进行修改，而从数据来源D’上做一些处理。按照这种思想，我们可以这样来看，如果对D’进行抽样，那么样本权重u实际上表示该样本在抽样中出现的次数，反映了它出现的概率；权重越大，出现概率越大。那么可以根据u值，对原样本集D进行一次重新的随机sampling，也就是带权重的随机抽样。sampling之后，会得到一个新的D’，D’中每个样本出现的几率与它权重u所占的比例应该是差不多接近的。因此，使用带权重的sampling操作，得到了新的样本数据集D’，可以直接代入决策树进行训练，从而无需改变决策树算法结构。这种对数据本身进行修改而不更改算法结构的方法非常重要！

所以，AdaBoost-DTree结合了AdaBoost和DTree，但是做了一点小小的改变，就是使用sampling替代权重$u^{(t)}$，效果是相同的。

上面我们通过使用sampling，将不同的样本集代入决策树中，得到不同的$g_t$。除此之外，我们还要确定每个$g_t$所占的权重$α_t$。之前我们在AdaBoost中已经介绍过，首先算出每个$g_t$的错误率$ϵ_t$，然后计算权重：
$$
α_t=ln\lozenge t=ln\sqrt{\frac{1-\epsilon_{t}}{\epsilon_{t}}}
$$
如果现在有一棵完全长成的树（fully grown tree），由所有的样本$x_n$训练得到。若每个样本都不相同的话，一刀刀切割分支，直到所有的$x_n$都被完全分开。这时候，$E_{in}(g_t)=0$，加权的$E_{in}^{u}(g_t)=0$，而且$ϵ_t$也为0，从而得到权重$α_t=∞$。$α_t=∞$表示该$g_t$所占的权重无限大，相当于它一个就决定了$G$结构，而其它的$g_t$对$G$没有影响。

显然$α_t=∞$不是我们想看到的，因为"独裁"总是不好的，我们希望使用aggregation将不同的$g_t$结合起来，发挥集体智慧来得到最好的模型$G$。首先，我们来看一下什么原因造成了$α_t=∞$。有两个原因：一个是使用了所有的样本$x_n$进行训练；一个是树的分支过多，fully grown。针对这两个原因，我们可以对树做一些修剪（pruned），比如只使用一部分样本，这在sampling的操作中已经起到这类作用，因为必然有些样本没有被采样到。除此之外，我们还可以限制树的高度，让分支不要那么多，从而避免树fully grown。

因此，AdaBoost-DTree使用的是pruned DTree，也就是说将这些预测效果较弱的树结合起来，得到最好的$G$，避免出现"独裁"。

刚才我们说了可以限制树的高度，那索性将树的高度限制到最低，即只有1层高的时候，有什么特性呢？当树高为1的时候，整棵树只有两个分支，切割一次即可。如果impurity是binary classification error的话，那么此时的AdaBoost-DTree即AdaBoost-Stump决策树桩。也就是说AdaBoost-Stump是AdaBoost-DTree的一种特殊情况。

值得一提是，如果树高为1时，通常较难遇到$ϵ_t=0$的情况，且一般不采用sampling的操作，而是直接将权重u代入到算法中。这是因为此时的AdaBoost-DTree就相当于是AdaBoost-Stump，而AdaBoost-Stump就是直接使用u来优化模型的。

从优化的角度来看Adaboost

对于二分类问题,我们知道AdaBoost中的权重的迭代计算如下所示：
$$
\begin{align}
u_{n}^{t+1}&=u_{n}^{t}\cdot \lozenge t^{-y_ng_t(x_n)}\\
&=u_{n}^{t}\cdot exp(-y_n\alpha_tg_t(x_n)
\end{align}
$$
其中，对于incorrect样本，$y_ng_t(x_n)<0$，对于correct样本，$y_ng_t(x_n)<0$。从上式可以看出，$u_{n}^{t+1}$由$u_{n}^{t}$与某个常数相乘得到。所以，最后一轮更新的$u_{n}^{t+1}$可以写成$u_{n}^{1}$的级联形式，我们之前令$u_{n}^{1}=1/N$，则有如下推导:
$$
u_{n}^{T+1}=u_n^1\cdot\prod_{t=1}^{T}exp(-y_n\alpha_tg_t(x_n))=\frac{1}{N}\cdot exp(-y_n\sum_{t=1}^{T}\alpha_tg_t(x_n))
$$
上式中$\sum_{t=1}^{T}\alpha_tg_t(x_n)$被称为voting score，最终的模型$G=sign(\sum_{t=1}^{T}\alpha_tg_t(x_n))$。可以看出，在AdaBoost中，$u_{n}^{T+1}$与$exp(-y_n\alpha_tg_t(x_n))$成正比。

接下来我们继续看一下voting score中蕴含了哪些内容。
$$
G(x_n)=sign \left (\overbrace{\sum_{t=1}^{T} \underbrace{\alpha_t}_{w_i}\underbrace{g_t(x_n)}_{\phi _i(x_n)}}^{voting \ score}\right )
$$
voting score由许多$g_t(x_n)$乘以各自的系数$α_t$线性组合而成。从另外一个角度来看，我们可以把$g_t(x_n)$看成是对$x_n$的特征转换$ϕ_i(x_n)$，$α_t$就是线性模型中的权重$w_i$。看到这里，我们回忆起之前SVM中，$w$与$ϕ(x_n)$的乘积再除以$w$的长度就是margin，即点到边界的距离。另外，乘积项再与$y_n$相乘，表示点的位置是在正确的那一侧还是错误的那一侧。所以，回过头来，这里的voting score实际上可以看成是没有正规化（没有除以w的长度）的距离，即可以看成是该点到分类边界距离的一种衡量。从效果上说，距离越大越好，也就是说voting score要尽可能大一些。

我们再来看，若voting score与$y_n$相乘，则表示一个有对错之分的距离。也就是说，如果二者相乘是负数，则表示该点在错误的一边，分类错误；如果二者相乘是正数，则表示该点在正确的一边，分类正确。所以，我们算法的目的就是让$y_n$与voting score的乘积是正的，而且越大越好。那么在刚刚推导的$u_{n}^{T+1}$中，若$exp(−y_n(voting score))$越小越好，那么$u_{n}^{T+1}$越小越好。也就是说，如果voting score表现不错，与$y_n$的乘积越大的话，那么相应的$u_{n}^{T+1}$应该是最小的。

那么在AdaBoost中，随着每轮学习的进行，每个样本的$u_{n}^{t}$是逐渐减小的，直到$u_{n}^{T+1}$最小。以上是从单个样本点来看的。总体来看，所有样本的$u_{n}^{T+1}$之和应该也是最小的。我们的目标就是在最后一轮（T+1）学习后，让所有样本的$u_{n}^{T+1}$之和尽可能地小。$u_{n}^{T+1}$之和表示为如下形式：
$$
\sum_{n=1}^{N}u_{n}^{T+1}=\frac{1}{N}\sum_{n=1}^{N}exp \left ( -y_n\sum_{t=1}^{T}\alpha_tg_t(x_n) \right)
$$
上式中，$\sum_{t=1}^{T}\alpha_tg_t(x_n)$用s来表示，对于0/1 error：若ys<0，则err0/1=1；若ys>=0，则err0/1=0。如下图右边黑色折线所示。对于上式中提到的指数error，即$\hat{err_{ADA}}=exp(−ys)$，随着ys的增加，error单调下降，且始终落在0/1 error折线的上面。如下图右边蓝色曲线所示。很明显，$\hat{err_{ADA}}$可以看成是0/1 error的上界。所以，我们可以使用$\hat{err_{ADA}}$来替代0/1 error，能达到同样的效果。从这点来说，$\sum_{n=1}^{N}u_{n}^{T+1}$可以看成是一种error measure，而我们的目标就是让其最小化，求出最小值时对应的各个$α_t$和$g_t(x_n)$。

joey

下面我们来研究如何让$\sum_{n=1}^{N}u_{n}^{T+1}$取得最小值，思考是否能用梯度下降（gradient descent）的方法来进行求解。我们之前介绍过gradient descent的核心是在某点处做一阶泰勒展开：
$$
\mathop{\min}_{\left | v \right |=1}E_{in}(\boldsymbol{w}_t+\boldsymbol{\eta}\boldsymbol{v} )\approx E_{in}(\boldsymbol{w_t})+\eta\cdot\boldsymbol{v}^T\triangledown E_{in}(\boldsymbol{w}_t)
$$
其中，$\boldsymbol{w_t}$是泰勒展开的位置，$\boldsymbol{v}$是所要求的下降的最好方向，它是梯度$\triangledown E_{in}(\boldsymbol{w}_t)$的反方向，而η是每次前进的步长。则每次沿着当前梯度的反方向走一小步，就会不断逼近谷底（最小值）。这就是梯度下降算法所做的事情。

现在，我们对$\hat{E}_{ADA}$做梯度下降算法处理，区别是这里的方向是一个函数$g_t$，而不是一个向量$\boldsymbol{w_t}$。其实，函数和向量的唯一区别就是一个下标是连续的，另一个下标是离散的，二者在梯度下降算法应用上并没有大的区别。因此，按照梯度下降算法的展开式，做出如下推导：
$$
\begin{align}
\mathop{\min}_{h}\hat{E}_{ADA}&=\frac{1}{N}\sum_{n=1}^{N}exp\left( -y_n\left( \sum_{\tau=1}^{t-1}\alpha_{\tau}g_{\tau}(\boldsymbol{x}_n)+\eta h(\boldsymbol{x}_n)\right) \right )\\
&=\sum_{n=1}^{N}u_n^{t}\cdot exp(-y_n\eta h(\boldsymbol{x}_n))
\end{align}
$$
对函数$exp(-y_n\eta h(\boldsymbol{x}_n))$在$-y_n\eta h(\boldsymbol{x}_n)=0$做泰勒展开，上式为
$$
\begin{align}
\mathop{\min}_{h}\hat{E}_{ADA}
&\approx \sum_{n=1}^{N}u_n^{t}(1-y_n\eta h(x_n))\\
&=\sum_{n=1}^{N}u_n^{t}-\eta \sum_{n=1}^{N}u_n^{t}y_nh(x_n)
\end{align}
$$
上式中，$h(x_n)$表示当前的方向，它是一个$g_t$，η是沿着当前方向前进的步长。我们要求出这样的$h(x_n)$和η，使得$\hat{E}_{ADA}$是在不断减小的。当$\hat{E}_{ADA}$取得最小值的时候，那么所有的方向即最佳的$h(x_n)$和η就都解出来了。上述推导使用了在$-y_n\eta h(\boldsymbol{x}_n)=0$处的一阶泰勒展开近似。这样经过推导之后，$\hat{E}_{ADA}$被分解为两个部分，一个是前N个u之和$\sum_{n=1}^{N}u_n^{t}$，也就是当前所有的$E_{in}$之和；另外一个是包含下一步前进的方向$h(x_n)$和步进长度η的项$-\eta \sum_{n=1}^{N}u_n^{t}y_nh(x_n)$。$\hat{E}_{ADA}$的这种形式与gradient descent的形式基本是一致的。

那么接下来，如果要最小化$\hat{E}_{ADA}$的话，就要让第二项$-\eta \sum_{n=1}^{N}u_n^{t}y_nh(x_n)$越小越好。则我们的目标就是找到一个好的$h(x_n)$（即好的方向）来最小化$\sum_{n=1}^{N}u_n^{t}(-y_nh(x_n))$，此时先忽略步进长度η。

对于二分类问题，$y_n$和$h(x_n)$均限定取值-1或+1两种。我们对$\sum_{n=1}^{N}u_n^{t}(-y_nh(x_n))$做一些推导和平移运算：
joey

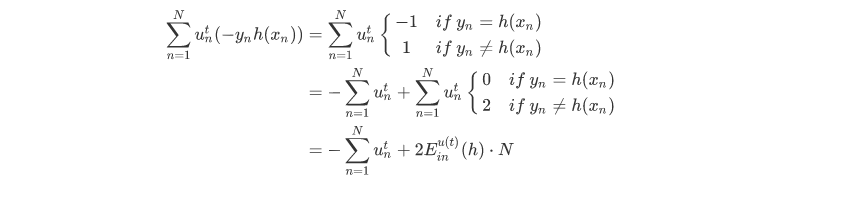
最终$\sum_{n=1}^{N}u_n^{t}(-y_nh(x_n))$化简为两项组成，一项是$-\sum_{n=1}^{N}u_n^{t}$；另一项是$2E_{in}^{u(t)}(h)\cdot N$。则最小化$\sum_{n=1}^{N}u_n^{t}(-y_nh(x_n))$就转化为最小化$E_{in}^{u(t)}(h)$。要让$E_{in}^{u(t)}(h)$最小化，正是由AdaBoost中的base algorithm所做的事情。所以说，AdaBoost中的base algorithm正好帮我们找到了梯度下降中下一步最好的函数方向。

从gradient descent角度验证了AdaBoost中使用base algorithm得到的$g_t$就是让$\hat{E}_{ADA}$减小的方向，只不过这个方向是一个函数而不是向量。

在解决了方向问题后，我们需要考虑步进长度η如何选取。方法是在确定方向$g_t$后，选取合适的η，使$\hat{E}_{ADA}$取得最小值。也就是说，把$\hat{E}_{ADA}$看成是步进长度η的函数，目标是找到$\hat{E}_{ADA}$最小化时对应的η值。

目的是找到在最佳方向上的最大步进长度，也就是steepest decent。我们先把$\hat{E}_{ADA}$表达式写下来：
$$
\hat{E}_{ADA}=\sum_{n=1}^{N}u_n^{t}\cdot exp(-y_n\eta g_t(\boldsymbol{x}_n))
$$
当$y_n=g_t(x_n)$时：$u_n^{t}\cdot exp(-\eta)$

当$y_n\neq g_t(x_n)$时：$u_n^{t}\cdot exp(+\eta)$

因此，
$$
\hat{E}_{ADA}=\sum_{n=1}^{N}u_n^{t}\cdot ((1-\epsilon_t)exp(-\eta)+\epsilon_texp(+\eta))
$$
然后对η求导，令$\frac{\partial \hat{E}_{ADA}}{\partial \eta}=0$，得：
$$
\eta_t=\sqrt{\frac{1-\epsilon_{t}}{\epsilon_{t}}}=\alpha_t
$$
由此看出，最大的步进长度就是$α_t$，即AdaBoost中计算$g_t$所占的权重。所以，AdaBoost算法所做的其实是在gradient descent上找到下降最快的方向和最大的步进长度。这里的方向就是$g_t$，它是一个函数，而步进长度就是$α_t$。也就是说，在AdaBoost中确定$g_t$和$α_t$的过程就相当于在gradient descent上寻找最快的下降方向和最大的步进长度。

Gradient Boosting

前面我们从gradient descent的角度来重新介绍了AdaBoost的最优化求解方法。整个过程可以概括为：
$$
\mathop{\min}_{\eta}\mathop{\min}_{h}\hat{E}_{ADA}=\frac{1}{N}\sum_{n=1}^{N}exp\left( -y_n\left( \sum_{\tau=1}^{t-1}\alpha_{\tau}g_{\tau}(\boldsymbol{x}_n)+\eta h(\boldsymbol{x}_n)\right) \right )
$$
以上是针对binary classification问题。如果往更一般的情况进行推广，对于不同的error function，比如logistic error function或者regression中的squared error function，那么这种做法是否仍然有效呢？这种情况下的GradientBoost可以写成如下形式：
$$
\mathop{\min}_{\eta}\mathop{\min}_{h}\hat{E}_{ADA}=\frac{1}{N}\sum_{n=1}^{N}err\left(\left( \sum_{\tau=1}^{t-1}\alpha_{\tau}g_{\tau}(\boldsymbol{x}_n)+\eta h(\boldsymbol{x}_n)\right), y_n \right )
$$
仍然按照gradient descent的思想，上式中，$h(x_n)$是下一步前进的方向，η是步进长度。此时的error function不是前面所讲的exp了，而是任意的一种error function。因此，对应的hypothesis也不再是binary classification，最常用的是实数输出的hypothesis，例如regression。最终的目标也是求解最佳的前进方向$(x_n)$和最快的步进长度η。

以regression为例，它的表达式如下所示：
$$
\mathop{\min}_{\eta}\mathop{\min}_{h}\hat{E}_{ADA}=\frac{1}{N}\sum_{n=1}^{N}err\left(\left( \underbrace{\sum_{\tau=1}^{t-1}\alpha_{\tau}g_{\tau}(\boldsymbol{x}_n)}_{s_n}+\eta h(\boldsymbol{x}_n)\right), y_n \right )
$$
其中，$err(s,y)=(s-y)^2$

我们把上式进行一阶泰勒展开，写成梯度的形式：
$$
\begin{align}
\mathop{\min}_{h}...&\approx \mathop{\min}_{h}\frac{1}{N}\sum_{n=1}^{N}err(s_n,y_n)+\frac{1}{N}\sum_{n=1}^{N}\eta h(x_n)\frac{\partial err(s,y_n)}{\partial s}|_{s=s_n}\\
&=\mathop{\min}_{h}constants+\frac{\eta}{N}\sum_{n=1}^{N}h(x_n)\cdot 2(s_n-y_n)
\end{align}
$$
上式中，由于regression的error function是squared的，所以，对s的导数就是$2(s_n-y_n)$。很明显，要使上式最小化，只要令$h(x_n)$是梯度$2(s_n-y_n)$的反方向就行了，即$h(x_n)=2(s_n-y_n)$。但是直接这样赋值，并没有对$h(x_n)$的大小进行限制，一般不直接利用这个关系求出$h(x_n)$。

实际上$h(x_n)$的大小并不重要，因为有步进长度η。那么，我们上面的最小化问题中需要对$h(x_n)$的大小做些限制。限制$h(x_n)$的一种简单做法是把$h(x_n)$的大小$h^2(x_n)$当成一个惩罚项添加到上面的最小化问题中，这种做法与regularization类似。如下图所示，经过推导和整理，忽略常数项，我们得到最关心的式子是：
$$
min\sum_{n=1}^{N}(h(x_n)-(y_n-s_n))^2
$$
上式是一个完全平方项之和，$(y_n-s_n)$表示当前第n个样本真实值和预测值的差，称之为残差。残差表示当前预测能够做到的效果与真实值的差值是多少。那么，如果我们想要让上式最小化，求出对应的$h(x_n)$的话，只要让$h(x_n)$尽可能地接近余数$(y_n-s_n)$即可。在平方误差上尽可能接近其实很简单，就是使用regression的方法，对所有N个点$(x_n,(y_n-s_n))$做squared-error的regression，得到的回归方程就是我们要求的$g_t(x_n)$。

在求出最好的方向函数$g_t(x_n)$之后，就要来求相应的步进长度η。表达式如下：
$$
\mathop{\min}_{\eta}\hat{E}_{ADA}=\frac{1}{N}\sum_{n=1}^{N}err\left(\left( \underbrace{\sum_{\tau=1}^{t-1}\alpha_{\tau}g_{\tau}(\boldsymbol{x}_n)}_{s_n}+\eta h(\boldsymbol{x}_n)\right), y_n \right )
$$
其中，$err(s,y)=(s-y)^2$，将上式化简下得到
$$
\mathop{\min}_{\eta}\frac{1}{N}\sum_{n=1}^{N}(s_n+\eta g_t(x_n)-y_n)^2=\frac{1}{N}\sum_{n=1}^{N}((y_n-s_n)-\eta g_t(x_n))^2
$$
上式中也包含了残差$(y_n-s_n)$，其中$g_t(x_n)$可以看成是$x_n$的特征转换，是已知量。那么，如果我们想要让上式最小化，求出对应的η的话，只要让$\eta g_t(x_n)$尽可能地接近残差$(y_n-s_n)$即可。显然，这也是一个regression问题，而且是一个很简单的形如y=ax的线性回归，只有一个未知数η。只要对所有N个点$(\eta g_t(x_n),y_n−s_n)$做squared-error的linear regression，求出η即可。

将上述这些概念合并到一起，我们就得到了一个最终的演算法Gradient Boosted Decision Tree(GBDT)。可能有人会问，我们刚才一直没有说到Decison Tree，只是讲到了GradientBoost啊？下面我们来看看Decison Tree究竟是在哪出现并使用的。其实刚刚我们在计算方向函数gtgt的时候，是对所有N个点$(x_n,(y_n-s_n))$做squared-error的regression。那么这个回归算法就可以是决策树C&RT模型（决策树也可以用来做regression）。这样，就引入了Decision Tree，并将GradientBoost和Decision Tree结合起来，构成了真正的GBDT算法。GBDT算法的基本流程图如下所示：

joey

值得注意的是，$s_n$的初始值一般均设为0，即$s_1=s_2=⋯=s_N=0$。每轮迭代中，方向函数$g_t$通过C&RT算法做regression，进行求解；步进长度η通过简单的单参数线性回归进行求解；然后每轮更新sn的值，即$s_n←s_n+α_tg_t(x_n)$。T轮迭代结束后，最终得到$G(x)=\sum_{t=1}^{T}\alpha_tg_t(x)$。

值得一提的是，本节课第一部分介绍的AdaBoost-DTree是解决binary classification问题，而此处介绍的GBDT是解决regression问题。二者具有一定的相似性，可以说GBDT就是AdaBoost-DTree的regression版本。

Summary of Aggregation Models

我们已经介绍完所有的aggregation模型了。接下来，我们将对这些内容进行一个简单的总结和概括。

首先，我们介绍了blending。blending就是将所有已知的$g_t$ aggregate结合起来，发挥集体的智慧得到$G$。值得注意的一点是这里的$g_t$都是已知的。blending通常有三种形式：

uniform：简单地计算所有$g_t$的平均值
non-uniform：所有$g_t$的线性组合
conditional：所有$g_t$的非线性组合

其中，uniform采用投票、求平均的形式更注重稳定性；而non-uniform和conditional追求的更复杂准确的模型，但存在过拟合的危险。

刚才讲的blending是建立在所有$g_t$已知的情况。那如果所有$g_t$未知的情况，对应的就是learning模型，做法就是一边学$g_t$，一边将它们结合起来。learning通常也有三种形式（与blending的三种形式一一对应）：

Bagging：通过bootstrap方法，得到不同$g_t$，计算所有$g_t$的平均值
AdaBoost：通过re-weighting样本权重方法，得到不同$g_t$，所有$g_t$的线性组合
Decision Tree：通过数据分割的形式得到不同的$g_t$，所有$g_t$的非线性组合

除了这些基本的aggregation模型之外，我们还可以把某些模型结合起来得到新的aggregation模型。例如，Bagging与Decision Tree结合起来组成了Random Forest。Random Forest中的Decision Tree是比较“茂盛”的树，即每个树的$g_t$都比较强一些。AdaBoost与Decision Tree结合组成了AdaBoost-DTree。AdaBoost-DTree的Decision Tree是比较“矮弱”的树，即每个树的$g_t$都比较弱一些，由AdaBoost将所有弱弱的树结合起来，让综合能力更强。同样，GradientBoost与Decision Tree结合就构成了经典的算法GBDT。

Aggregation的核心是将所有的$g_t$结合起来，融合到一起，即集体智慧的思想。这种做法之所以能得到很好的模型G，是因为aggregation具有两个方面的优点：cure underfitting和cure overfitting。

第一，aggregation models有助于防止欠拟合（underfitting）。它把所有比较弱的$g_t$结合起来，利用集体智慧来获得比较好的模型G。aggregation就相当于是feature transform，来获得复杂的学习模型。

第二，aggregation models有助于防止过拟合（overfitting）。它把所有$g_t$进行组合，容易得到一个比较中庸的模型，类似于SVM的large margin一样的效果，从而避免一些极端情况包括过拟合的发生。从这个角度来说，aggregation起到了regularization的效果。

由于aggregation具有这两个方面的优点，所以在实际应用中aggregation models都有很好的表现。

总结

主要介绍了Gradient Boosted Decision Tree。首先讲如何将AdaBoost与Decision Tree结合起来，即通过sampling和pruning的方法得到AdaBoost-D Tree模型。然后，我们从optimization的角度来看AdaBoost，找到好的hypothesis也就是找到一个好的方向，找到权重αα也就是找到合适的步进长度。接着，我们从binary classification的0/1 error推广到其它的error function，从Gradient Boosting角度推导了regression的squared error形式。Gradient Boosting其实就是不断迭代，做residual fitting。并将其与Decision Tree算法结合，得到了经典的GBDT算法。最后，我们将所有的aggregation models做了总结和概括，这些模型有的能防止欠拟合有的能防止过拟合，应用十分广泛。

思考

$$
\mathop{\min}_{\eta}\mathop{\min}_{h}\hat{E}_{ADA}=\frac{1}{N}\sum_{n=1}^{N}exp\left( -y_n\left( \sum_{\tau=1}^{t-1}\alpha_{\tau}g_{\tau}(\boldsymbol{x}_n)+\eta h(\boldsymbol{x}_n)\right) \right )
$$

Q:为什么可以对上面这个式子做梯度下降??这个函数是关于h(x)的凸函数吗？如何证明？

A:前向分步算法+泰勒一阶展开决定的。跟凸函数无关

个人总结

Adaboost+decision就是统计学习方法第147页说的提升树

说白了，adaboost、提升树、gbdt 就是加法模型+前向分步算法

adaboost用于处理二分类问题，损失函数为指数损失函数，且有样本权重的概念，基模型的权重是根据加权误分类率决定的

gbdt不仅可用于分类，还可用于回归，损失函数可以为平方损失或其他一般的损失函数，基模型的权重是通过解一个一维最优化问题得到的

其实adaboost的样本权重和gbdt的上一步模型的残差本质上是一个东西

加法模型+前向分步算法

加法模型为
$$
G(x)=\sum_{t=1}^{T}\alpha_tg_t(x;\theta_t)
$$
其中，$g_t(x;\theta_t)$为基函数，$\theta_t$为基函数的参数，$\alpha_t$为基函数的系数。

在给定训练数据和损失函数$L(y,G(x))$的条件下，学习加法模型成为经验风险最小化即损失函数最小化问题：
$$
\mathop{\min}_{\alpha_t,\theta_t}\sum_{i=1}^{N}L\left (y_i,\sum_{t=1}^{T}\alpha_tg_t(x_i;\theta_t) \right)
$$
通常这是一个复杂的优化问题，前向分步算法求解这一优化问题的想法是：因为学习的是加法模型，如果能从前向后，每一步只学习一个基函数及其系数，逐步逼近优化目标函数式(19)，那么就可以简化优化的复杂度，具体的，每一步只需极小化如下损失函数就可以得到每一步的$\alpha_t$和$\theta_t$：
$$
(\alpha_t,\theta_t)=\mathop{\arg \min}_{\alpha,\theta}\sum_{i=1}^{N}L\left (y_i,G_{t-1}(x_i)+\alpha g(x_i;\theta) \right)
$$
这样，前向分步算法将同时求解从t=1到T所有参数$\alpha_t,\theta_t$的优化问题转化为逐次求解各个$\alpha_t,\theta_t$的优化问题。

adaboost算法就是由前向分步算法推导出来的

提升树

boosting（提升方法）实际就是加法模型（即基函数的线性组合）与前向分步算法。

以决策树为基函数的提升方法成为提升树，对分类问题决策树是二叉分类树，对回归问题决策树是二叉回归树。

提升树模型可以表示为决策树的加法模型：
$$
f_M(x)=\sum_{m=1}^{M}T(x;\Theta_m)
$$
其中，$T(x;\Theta_m)$表示决策树，$\Theta_m$为决策树的参数，M为树的个数，注意这里每棵树前面没有系数$\alpha_t$，这是因为系数可以包含在决策树的输出中

针对不同问题的提升树学习算法，其主要区别在于使用的损失函数不同，包括用平方误差损失函数的回归问题，用指数损失函数的分类问题，用一般损失函数的一般决策问题。

对于二分类问题，且损失函数为指数损失函数的时候，提升树算法即基分类器为二分类树的adaboost算法。
对于回归问题，每棵树可以表示成：

$$
T(x;\Theta_m)=\sum_{j=1}^{J}c_jI(x\in R_j)
$$

在前向分步算法的第m步，给定当前模型$f_{m-1}(x)$，需求解
$$
\hat{\Theta}_m=\mathop{\arg \min}_{\Theta}\sum_{i=1}^{N}L\left (y_i,f_{m-1}(x_i)+T(x_i;\Theta)\right)
$$
得到$\hat{\Theta}_m$，即第m棵树的参数。

当采用平方误差损失函数时，

$$
L(y,f(x))=(y-f(x))^2
$$
第m步的损失为
$$
\begin{align}
L\left (y,f_{m-1}(x)+T(x;\Theta_m)\right)&=\left [y-f_{m-1}(x)-T(x;\Theta_m)\right]^2\\
&=[r-T(x;\Theta_m)]^2
\end{align}
$$
这里，
$$
r=y-f_{m-1}(x)
$$
是当前模型拟合数据的残差，所以，对平方损失回归问题的提升树算法来说，只需简单地拟合当前模型的残差，就可以得到第m棵树的最优参数$\Theta_m$。

那么问题来了，对于平方损失回归问题的提升树算法来说，只需简单地拟合当前模型的残差，就可以让损失函数最小，从而得到第m棵树的最优参数$\Theta_m$；但是对于一般的损失函数，我们有时候不知道通过拟合什么来让损失函数最小，得到让损失函数最小的最优参数$\Theta_m$，这时候该怎么办呢？

梯度提升树

但是对于一般的损失函数，我们有时候不知道通过拟合什么来让损失函数最小，得到让损失函数最小的最优参数$\Theta_m$，这时候该怎么办呢？

这句话怎么理解呢？可以回忆一下在逻辑斯蒂回归中交叉熵损失函数最小时的参数$\mathbf{w}$，也就是$\nabla E_{in}(\mathbf{w})=0$时的参数$\mathbf{w}$，但是这个方程没有闭式解，即我们不知道最优的$\mathbf{w}$长什么样子来让损失函数最小。现在说清楚了吧。

"一下子优化"和“逐步优化”

问题又来了，既然很难一下子得到最优的$g_t$，该怎么做呢?

一个很自然的想法是，既然这个问题可以类比逻辑斯蒂回归中的损失函数最优化问题，那么我们看看在lr中是怎么解决这个问题不就行了吗？是的，没错！

逻辑斯蒂回归中解决这个问题的方法是梯度下降法，由于损失函数是凸函数，只要保证第t+1轮的损失比第t轮的小$E_{in}(\mathbf{w}_{t+1})<E_{in}(\mathbf{w}_{t})$，那么经过一定次数T的迭代后，就可以保证$E_{in}(\mathbf{w}_{T})$达到最小。

推广到这个问题，我们只要保证第t轮加入的基函数$g_t(x)$加入到当前模型$G_{t-1}(x)$后的损失比当前模型$G_{t-1}(x)$的损失小，那么经过一定次数T的迭代后，就可以保证最后的模型$G_{T}(x)$的损失很小。

怎样保证$Loss(G_{t-1}(x)+\alpha_tg_t(x))<Loss(G_{t-1}(x))$呢？泰勒展开！！

观察下Loss的表达式
$$
\sum_{i=1}^{N}L(y_i,G_{t-1}(x_i)+\alpha_tg_t(x_i))
$$
对这个函数在$G(x)=G_{t-1}(x)$处泰勒一阶展开，
$$
\sum_{i=1}^{N}L(y_i,G_{t-1}(x_i)+\alpha_tg_t(x_i))=\sum_{i=1}^{N}L(y_i,G_{t-1}(x_i))+\alpha_tg_t(x_i)\left [ \frac{\partial L(y_i,G(x_i))}{\partial G(x_i) }\right ]_{G(x)=G_{t-1}(x)}
$$
由于$\alpha_t$是大于0的，若
$$
g_t(x_i)=-\left [ \frac{\partial L(y_i,G(x_i))}{\partial G(x_i) }\right ]_{G(x)=G_{t-1}(x)}
$$
则
$$
\sum_{i=1}^{N}L(y_i,G_{t-1}(x_i)+\alpha_tg_t(x_i))\leq\sum_{i=1}^{N}L(y_i,G_{t-1}(x_i))
$$
式(28)就告诉了我们如何得到$g_t(x)$，这是一个回归问题。

有了$g_t(x)$后，很容易得到$\alpha_t$，这是一个一维搜索问题。

思考下lr中的梯度下降和gbdt的梯度提升，下降的是损失，提升的是表现，本质都是逐步降低损失值。因此梯度提升树叫做梯度下降树也无妨~~

参考

红色石头机器学习之路

数据挖掘面试题之梯度提升树

gbdt源码

李航统计学习方法

林轩田机器学习技法