基于流行度的推荐
基于流行度的算法非常简单粗暴,类似于各大新闻、微博热榜等,根据PV、UV、日均PV或分享率等数据来按某种热度排序来推荐给用户。
这种算法的优点是简单,适用于刚注册的新用户。缺点也很明显,它无法针对用户提供个性化的推荐。基于这种算法也可做一些优化,比如加入用户分群的流行度排序,例如把热榜上的体育内容优先推荐给体育迷,把政要热文推给热爱谈论政治的用户。
协同过滤算法
CF算法包括基于用户的CF(User-based CF)和基于物品的CF(Item-based CF)。
基于用户的CF原理如下:
1. 分析各个用户对item的评价(通过浏览记录、购买记录等);
2. 依据用户对item的评价计算得出所有用户之间的相似度;
3. 选出与当前用户最相似的N个用户;
4. 将这N个用户评价最高并且当前用户又没有浏览过的item推荐给当前用户。
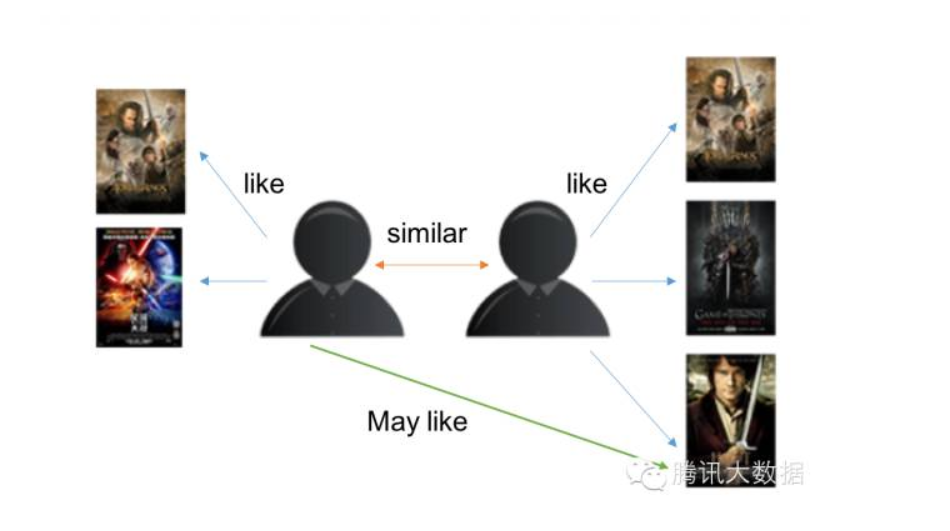
基于物品的CF原理大同小异,只是主体在于物品:
1. 分析各个用户对item的浏览记录。
2. 依据浏览记录分析得出所有item之间的相似度;
3. 对于当前用户评价高的item,找出与之相似度最高的N个item;
4. 将这N个item推荐给用户。
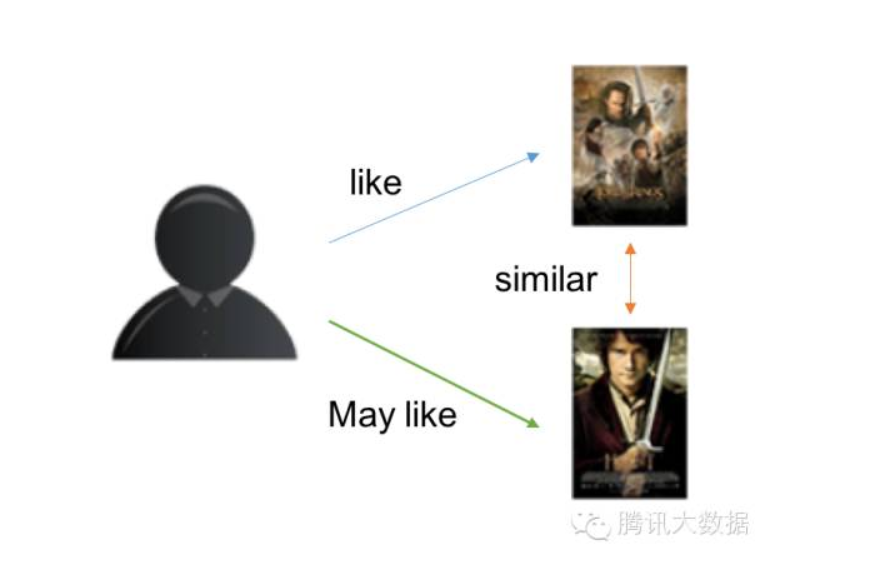
举个栗子,基于用户的CF算法大致的计算流程如下:
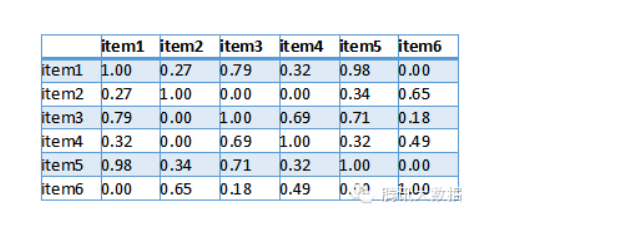
首先我们根据网站的记录得到一个用户与item的关联矩阵,如下:
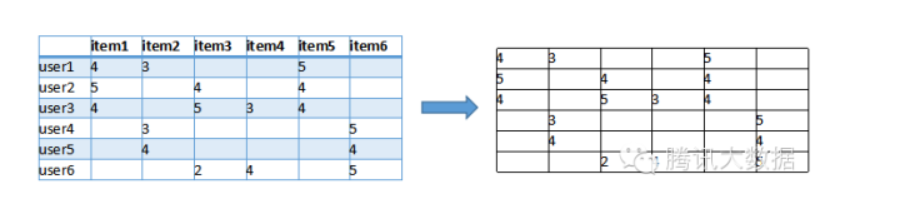
图中,行是不同的用户,列是所有物品,(x, y)的值则是x用户对y物品的评分(喜好程度)。我们可以把每一行视为一个用户对物品偏好的向量,然后计算每两个用户之间的向量距离,这里我们用余弦相似度来算(还可以用皮尔逊相关系数、欧氏距离、曼哈顿距离来度量向量相似度):
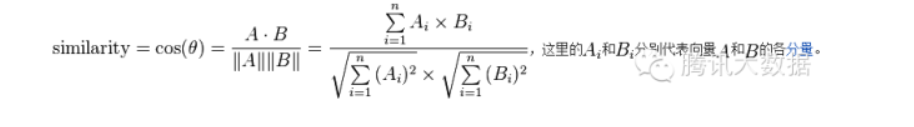
然后得出用户向量之间相似度如下,其中值越接近1表示这两个用户越相似:
最后,我们要为用户1推荐物品,则找出与用户1相似度最高的N名用户评价的物品,去掉用户1评价过的物品,则是推荐结果。
基于物品的CF计算方式大致相同,只是关联矩阵变为了item和item之间的关系。
我们可以看到,CF算法确实简单,而且很多时候推荐也是很准确的。然而它也存在一些问题:
- 依赖于准确的用户评分;
- 在计算的过程中,那些大热的物品会有更大的几率被推荐给用户;
- 冷启动问题。当有一名新用户或者新物品进入系统时,推荐将无从依据;
- 在一些item生存周期短(如新闻、广告)的系统中,由于更新速度快,大量item不会有用户评分,造成评分矩阵稀疏,不利于这些内容的推荐。
该算法的好处是:
- 能起到意想不到的推荐效果, 经常能推荐出来一些惊喜结果
- 能够有效挖掘出位于长尾部分的item
- 只依赖用户行为, 不需要对内容进行深入了解, 使用范围广
Item-CF和User-CF选择
- user和item数量分布以及变化频率
- 如果user数量远远大于item数量, 采用Item-CF效果会更好, 因为同一个item对应的打分会比较多, 而且计算量会相对较少
- 如果item数量远远大于user数量, 则采用User-CF效果会更好, 原因同上
- 在实际生产环境中, 有可能因为用户无登陆, 而cookie信息又极不稳定, 导致只能使用item-cf
- 如果用户行为变化频率很慢(比如小说), 用User-CF结果会比较稳定
- 如果用户行为变化频率很快(比如新闻, 音乐, 电影等), 用Item-CF结果会比较稳定
- 相关和惊喜的权衡
- item-based出的更偏相关结果, 出的可能都是看起来比较类似的结果
- user-based出的更有可能有惊喜, 因为看的是人与人的相似性, 推出来的结果可能更有惊喜
- 数据更新频率和时效性要求
- 对于item更新时效性较高的产品, 比如新闻, 就无法直接采用item-based的CF, 因为CF是需要批量计算的, 在计算结果出来之前新的item是无法被推荐出来的, 导致数据时效性偏低;
- 但是可以采用user-cf, 再记录一个在线的用户item行为对, 就可以根据用户最近类似的用户的行为进行时效性item推荐;
- 对于像影视, 音乐之类的还是可以采用item-cf的
基于矩阵分解的算法
SVD分解
SVD的作用是将一个矩阵分解为三个矩阵相乘的形式。
| movie1 | movie2 | movie3 | movie4 | |
|---|---|---|---|---|
| user1 | 1 | |||
| user2 | 2 | 3 | ||
| user3 | 5 | 4 | ||
| user4 | 2 | 4 |
空余处表示数据集中没有对应用户和电影的信息。如果我们想使用SVD,可以将空余处都填为0.假设此矩阵为R.那么运用SVD可以得到$R=UΣV^T$。 如果我们只取前k个奇异值的话,就可以得到一个新的矩阵$R^{'}$,那么原来的空白处可能就不再为0,这就是对该user-moive对的预测。因为SVD有很多现成的算法,也不用迭代就可直接得到,所以使用比较方便。
但是我们会看到,上面方法有一个致命的缺陷,那就是将未知的评分全都设为0.这其实是极其不合理的,因为用户不给某个电影打分并不是很不喜欢(0分),而是有可能还没有看过这个电影。这样就加入了我们主观臆断的信息,最后造成错误。
如果用0填充缺失值后做SVD分解,分解后相乘得到的新矩阵应该和原矩阵是接近的,缺失值处应该基本还是0。所以我的理解应该不太对,感觉SVD分解应该和隐因子分解本质是一样的,因为3个矩阵相乘$UΣV^T$也可以写成2个矩阵相乘$QP^T$的形式,无非就是$Q=UΣ$,然后用梯度下降法求解。
基于隐因子的矩阵分解
基础的矩阵分解
算法的思想是:设用户对物品的偏好矩阵为$R$,$R$是一个$m \times n$的矩阵,我们可以将$R$分解为两个矩阵相乘的形式,即$R=QP^T$,我们的目的就是找到这两个矩阵:
1. 用户-潜在因子矩阵Q,表示不同的用户对于不用元素的偏好程度,1代表很喜欢,0代表不喜欢。以歌曲为例:
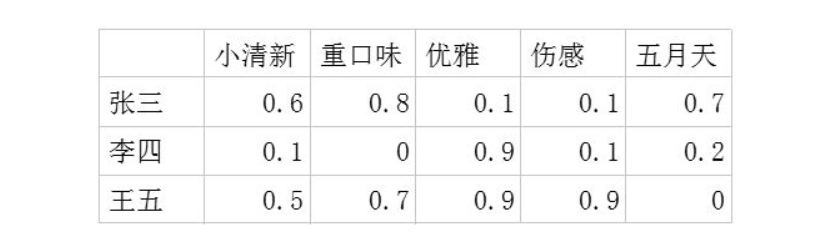
2. 潜在因子-音乐矩阵P,表示每种音乐含有各种元素的成分,比如下表中,音乐A是一个偏小清新的音乐,含有小清新这个Latent Factor的成分是0.9,重口味的成分是0.1,优雅的成分是0.2……
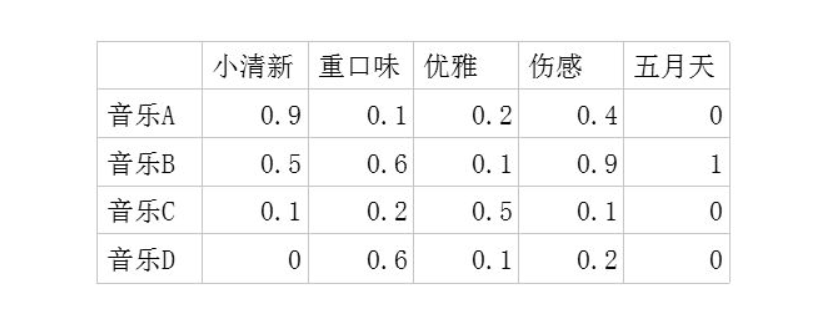
利用这两个矩阵,我们能得出张三对音乐A的喜欢程度是:张三对小清新的偏好$\times$音乐A含有小清新的成分+对重口味的偏好$\times$音乐A含有重口味的成分+对优雅的偏好$\times$音乐A含有优雅的成分+……
那么问题来了,我们如何确定这个Q和P?一个自然的想法就是让R'和真实的评分矩阵R尽可能地相等。那么这又有一个问题,那就是R有很多地方是没有评分的,如何判断和R'是否相等?那么我们在这里只计算有评分处的MSE。这样既没有使用额外的信息,又能判断两者是否接近。那么自然而然得就引入了我们的lost function:
$$
e_{ij}^2=(r_{ij}-\hat{r_{ij}})^2=(r_{ij}-\sum_{k=1}^{K}p_{ik}q_{kj})^2
$$
最终,需要求解所有的非空项的损失之和的最小值:
$$
min\ loss=min\ \sum_{r_{ij}is\ not\ null}e_{ij}^2
$$
对于上述的平方损失函数,可以通过梯度下降法求解,梯度下降法的核心步骤是
1. 求解损失函数的负梯度:
$$
\frac{\partial e_{ij}^2}{\partial p_{ik}}=-2(r_{ij}-\sum_{k=1}^{K}p_{ik}q_{kj})q_{kj}=-2e_{ij}q_{kj}
$$
$$
\frac{\partial e_{ij}^2}{\partial q_{kj}}=-2(r_{ij}-\sum_{k=1}^{K}p_{ik}q_{kj})p_{ik}=-2e_{ij}p_{ik}
$$
2. 根据负梯度的方向更新变量:
$$
p_{ik}^{'}=p_{ik}-\eta\frac{\partial e_{ij}^2}{\partial p_{ik}}=p_{ik}+2\eta e_{ij}q_{kj}
$$
$$
q_{kj}^{'}=q_{kj}-\eta\frac{\partial e_{ij}^2}{\partial q_{kj}}=q_{kj}+2\eta e_{ij}p_{ik}
$$
通过迭代,直到算法最终收敛。
加入正则项
通常在求解的过程中,为了能够有较好的泛化能力,会在损失函数中加入正则项,以对参数进行约束,加入L2正则的损失函数为:
$$
e_{ij}^2=(r_{ij}-\sum_{k=1}^{K}p_{ik}q_{kj})^2+\frac{\lambda}{2}\sum_{k=1}^{K}(p_{ik}^2+q_{kj}^2)
$$
1. 求解损失函数的负梯度:
$$
\frac{\partial e_{ij}^2}{\partial p_{ik}}=-2(r_{ij}-\sum_{k=1}^{K}p_{ik}q_{kj})q_{kj}=-2e_{ij}q_{kj}+\lambda p_{ik}
$$
$$
\frac{\partial e_{ij}^2}{\partial q_{kj}}=-2(r_{ij}-\sum_{k=1}^{K}p_{ik}q_{kj})p_{ik}=-2e_{ij}p_{ik}+\lambda q_{kj}
$$
2. 根据负梯度的方向更新变量:
$$
p_{ik}^{'}=p_{ik}+\eta(2 e_{ij}q_{kj}-\lambda p_{ik})
$$
$$
q_{kj}^{'}=q_{kj}+\eta(2 e_{ij}p_{ik}-\lambda q_{kj})
$$
通过迭代,直到算法最终收敛。
用上述的过程,我们可以得到矩阵$P_{m×k}$和$Q_{k×n}$,这样便可以为用户$i$对商品$j$进行打分:$\sum_{k=1}^{K}p_{ik}q_{kj}$
考虑偏置
那么进一步,为了实现更好的效果,我们要考虑每个个体打分的影响,因为有些用户打分偏高,有些用户打分偏低。同样对于电影和所有的评分。所以我们评分的计算公式应该改为:
$$
R_{ij} = \sum_{k=1}^{K}p_{ik}q_{kj} + mean + a_i +b_j
$$
其中mean是所有评分的平均值,$a_i$是用户i打分的平均值,$b_j$是电影j得分的平均值。其中mean认为是一个常数,而ai和bj都是需要优化的参数,需要加入到梯度的表达式中。
基于内容的推荐算法
CF算法看起来很好很强大,通过改进也能克服各种缺点。那么问题来了,假如我是个《指环王》的忠实读者,我买过一本《双塔奇兵》,这时库里新进了第三部:《王者归来》(即物品冷启动问题),那么显然我会很感兴趣。然而基于之前的算法,无论是用户评分还是书名的检索都不太好使,于是基于内容的推荐算法呼之欲出。
举个栗子,现在系统里有一个用户和一条新闻。通过分析用户的行为以及新闻的文本内容,我们提取出数个关键字,如下图:

将这些关键字作为属性,把用户和新闻分解成向量,如下图:
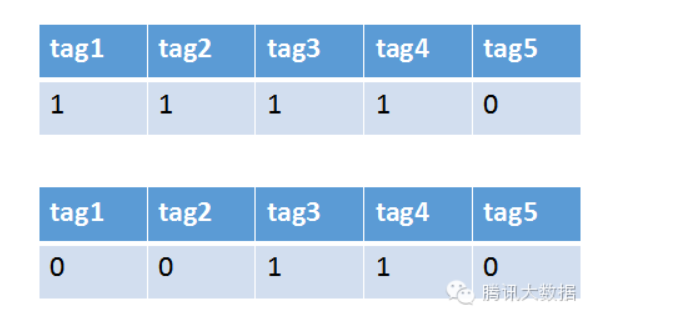
之后再计算向量距离,便可以得出该用户和新闻的相似度了。这种方法很简单,如果在为一名热爱观看英超联赛的足球迷推荐新闻时,新闻里同时存在关键字体育、足球、英超,显然匹配前两个词都不如直接匹配英超来得准确,系统该如何体现出关键词的这种“重要性”呢?这时我们便可以引入词权的概念。在大量的语料库中通过计算(比如典型的TF-IDF算法),我们可以算出新闻中每一个关键词的权重,在计算相似度时引入这个权重的影响,就可以达到更精确的效果,sim(user, item) = 文本相似度(user, item) * 词权
然而,经常接触体育新闻方面数据的同学就会要提出问题了:要是用户的兴趣是足球,而新闻的关键词是德甲、英超,按照上面的文本匹配方法显然无法将他们关联到一起。在此,我们可以引用话题聚类:
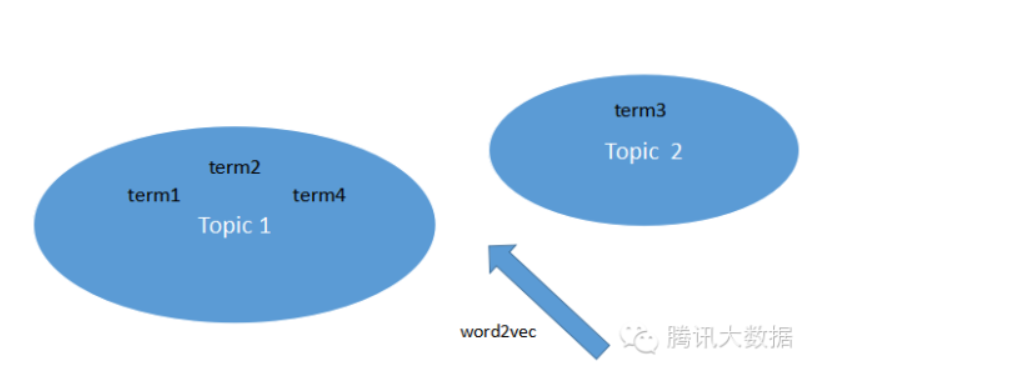
利用word2vec一类工具,可以将文本的关键词聚类,然后根据topic将文本向量化。如可以将德甲、英超、西甲聚类到“足球”的topic下,将lv、Gucci聚类到“奢侈品”topic下,再根据topic为文本内容与用户作相似度计算。
该算法的好处是:
- 不依赖于用户行为, 即不需要冷启动的过程, 随时到随时都能推荐
- 可以给出看起来比较合理的推荐解释
- item被推荐的时效性可以做得很高, 比如新闻类产品就需要用到该算法
该算法的坏处是:
- 需要理解item的内容, 对音频/视频等不好解析内容的就不好处理了
- 对于一次多义以及一义多词等情况处理起来比较复杂
- 容易出现同质化严重的问题, 缺乏惊喜
冷启动问题
- 用户冷启动:如何给新用户做个性化的推荐
- 物品冷启动:如何将新物品推荐给可能感兴趣的用户
- 系统冷启动:如何在新开发的网站上(无历史用户无历史物品)设计个性化推荐系统
解决方案:
- 提供非个性化的推荐:首先推荐热门排行榜,收集到一定的信息之后再切换为个性化推荐
- 粗粒度个性化:根据用户注册时提供的年龄性别等
- 社交账号:授权社交网路账号,导入好友信息,给用户推荐好友喜欢的物品
- 登录反馈:用户在登录的时候对一些物品进行反馈,以此收集兴趣
- 基于内容:新加入的物品基于内容推荐给喜欢过和他们相似的物品的用户
- 专家知识:进入专家知识,通过一定高校方式迅速建立物品的相关度表
基于机器学习模型的推荐
采用机器学习模型做预测。
混合算法
现实应用中,其实很少有直接用某种算法来做推荐的系统。在一些大的网站如Netflix,就是融合了数十种算法的推荐系统。我们可以通过给不同算法的结果加权重来综合结果,或者是在不同的计算环节中运用不同的算法来混合,达到更贴合自己业务的目的。
推荐结果评估
当推荐算法完成后,怎样来评估这个算法的效果?
CTR(点击率)、CVR(转化率)、停留时间等都是很直观的数据。在完成算法后,可以通过线下计算算法的RMSE(均方根误差)或者线上进行ABTest来对比效果。
参考
常见推荐算法科普
5类系统推荐算法,非常好使,非常全
推荐算法——基于矩阵分解的推荐算法
推荐系统——基于隐因子矩阵分解的协同过滤算法
知乎-网易云音乐的歌单推荐算法是怎样的?