Decision Tree算法的核心是通过递归的方式,将数据集不断进行切割,得到子分支,最终形成树的结构。随机森林(Random Forest)算法,它是之前介绍的Bagging和Decision Tree的结合。
Random Forest Algorithm
首先我们来复习一下之前介绍过的两个机器学习模型:Bagging和Decision Tree。Bagging是通过bootstrap的方式,从原始的数据集$D$中得到新的$\hat{D}$;然后再使用一些base algorithm对每个$\hat{D}$都得到相应的$g_t$;最后将所有的$g_t$通过投票uniform的形式组合成一个$G$,$G$即为我们最终得到的模型。Decision Tree是通过递归形式,利用分支条件,将原始数据集$D$切割成一个个子树结构,长成一棵完整的树形结构。Decision Tree最终得到的$G(x)$是由相应的分支条件$b(x)$和分支树$G_c(x)$递归组成。
Bagging和Decison Tree算法各自有一个很重要的特点。Bagging具有减少不同$g_t$的方差variance的特点。这是因为Bagging采用投票的形式,将所有$g_t$uniform结合起来,起到了求平均的作用,从而降低variance。而Decision Tree这种演算法的方差variance很大。这是因为一旦数据集$D_t$发生变化,Decision Tree每次切割的方式就会大不相同,而且切割之后分支包含的样本数在逐渐减少,所以它对不同的资料$D_t$会比较敏感一些,因此方差较大。
所以说,Bagging能减小variance,而Decision Tree的variance较大。如果把两者结合起来,能否发挥各自的优势,起到优势互补的作用呢?这就是我们接下来将要讨论的aggregation of aggregation,即使用Bagging的方式把众多的Decision Tree进行uniform结合起来。这种算法就叫做随机森林(Random Forest),它将完全长成的C&RT决策树通过bagging的形式结合起来,最终得到一个庞大的决策模型。
Random Forest算法流程为:
$for t=1,2,...,T$
- 从数据集$D$中通过bootstrap的方式抽样得到$N'$笔资料$\tilde{D_t}$
- 在$\tilde{D_t}$上学习得到一颗决策树$g_t$
$return G=uniform(g_t)$
Random Forest算法的优点主要有三个:
- 不同决策树可以由不同主机并行训练生成,效率很高;
- 随机森林算法继承了C&RT的优点;
- 将所有的决策树通过bagging的形式结合起来,避免了单个决策树造成过拟合的问题
以上是基本的Random Forest算法,我们再来看一下如何让Random Forest中决策树的结构更有多样性。
除了随机抽取资料获得不同$g_t$的方式之外,还有另外一种方法,就是随机抽取一部分特征。例如,原来有100个特征,现在只从中随机选取30个来构成决策树,那么每一轮得到的树都由不同的30个特征构成,每棵树都不一样。假设原来样本维度是d,则只选择其中的d’(d’小于d)个维度来建立决策树结构。这类似是一种从d维到d’维的特征转换,相当于是从高维到低维的投影,也就是说d’维z空间其实就是d维x空间的一个随机子空间(subspace)。通常情况下,d’远小于d,从而保证算法更有效率。Random Forest算法的作者建议在构建C&RT每个分支b(x)的时候,都可以重新选择子特征来训练,从而得到更具有多样性的决策树。
所以说,这种增强的Random Forest算法增加了random-subspace。
random-subspace相当于从整个属性集$A$中随机选择$n$个属性(特征){$a_1,a_2,...,a_n$},然后从这$n$个属性中选择一个最优属性进行划分,即随机抽取特征。除此之外,还可以将这$n$个特征{$a_1,a_2,...,a_n$},进行线性组合,即西瓜书第88页提到的多变量决策树(非叶节点不再是仅对某个属性,而是对属性的线性组合进行测试,换言之,每个非叶结点是一个形如$\sum_{i=1}^{n}w_i\cdot a_i=t$的线性分类器,其中,$w_i$是属性$a_i$的权重,$w_i$和$t$可在该结点所含的样本集和属性集上学得),这好比在二维平面上不止可以横着切和竖着切,也能斜着切。这种做法使子特征选择更加多样性。
所以,这里的Random Forest算法又有增强,由原来的random-subspace变成了random-combination。顺便提一下,这里的random-combination类似于perceptron模型。
Out-Of-Bag Estimate
通过bootstrap得到新的数据集$D_t$,再由$D_t$训练不同的$g_t$。我们知道$D_t$中包含了原样本集$D$中的一些样本,但也有些样本没有涵盖进去。如下表所示,不同的$g_t$下,红色的表示在$D_t$中没有这些样本。例如对$g_1$来说,(x2,y2)和(x3,y4)没有包含进去,对$g_2$来说,(x1,y1)和(x2,y2)没有包含进去,等等。每个$g_t$中,红色*表示的样本被称为out-of-bag(OOB) example。
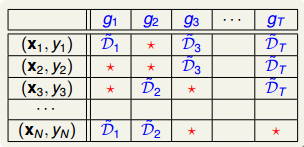
首先,我们来计算OOB样本到底有多少。假设bootstrap的数量N’=N,那么某个样本(xn,yn)是OOB的概率是:
$$
(1-\frac{1}{N})^N=\frac{1}{(1+\frac{1}{N-1})^N}\approx \frac{1}{e}
$$
由上述推导可得,每个$g_t$中,OOB数目大约是$\frac{1}{e}$,即大约有三分之一的样本没有在bootstrap中被抽到。
回顾一下之前的validation:将数据集$D$划分为$D_{train}$和$D_{val}$,二者没有交集,用$D_{train}$来训练模型,得到$g_t^-$,用
$D_{val}$来验证$g_t^-$的好坏。在随机森林中,每次bootstrap采样后得到的数据集$D_t$可以看做$D_{train}$,而OOB样本集可以看成$D_{val}$,那么我们就可以使用OOB样本来验证$g_t$的好坏。但是,通常我们并不需要对单个$g_t$进行验证。因为我们更关心的是由许多$g_t$组合成的$G$,即使$g_t$表现不太好,只要$G$表现足够好就行了。
那么问题就转化成了如何使用OOB来验证$G$的好坏。方法是先看每一个样本(xn,yn)是哪些$g_t$的OOB资料,然后计算其在这些$g_t$上的表现,最后将所有样本的表现求平均即可。例如,样本(xN,yN)是$g_2,g_3,g_T$的OOB,则可以计算$G_{N}^{-}$在(xN,yN)上的表现为:
$$
G_{N}^{-}(x)=avg(g_2,g_3,g_T)
$$
这种做法我们并不陌生,就像是Leave-One-Out Cross Validation,每次只对一个样本进行$g−$验证一样,只不过这里选择的是每个样本是哪些$g_t$的OOB,然后再分别进行$G_{n}^{-}(x)$的验证。每个样本都当成验证资料一次(与留一法相同),最后计算所有样本的平均表现:
$$
E_{oob}(G)=\frac{1}{N}\sum_{n=1}^{N}err(y_n,G_{n}^{-}(x_n))
$$
$E_{oob}(G)$估算的就是$G$的表现好坏,我们把$E_{oob}(G)$称为bagging或者Random Forest的self-validation。
这种self-validation相比于validation来说还有一个优点就是它不需要重复训练。在validation中,通过$D_{val}$选择到表现最好的$g_m^-$之后,还需要在$D_{train}$和$D_{val}$组成的所有样本集$D$上重新对该模型$g_m^-$训练一次,以得到最终的模型系数。但是self-validation在调整随机森林算法相关系数并得到最小的$E_{oob}$之后,就完成了整个模型的建立,无需重新训练模型。随机森林算法中,self-validation在衡量$G$的表现上通常相当准确。
Feature Selection
如果样本资料特征过多,假如有10000个特征,但并不是每一个特征都是有用的,这时候就需要舍弃部分特征。通常来说,需要移除的特征分为两类:
- 一类是冗余特征,即特征出现重复,例如“年龄”和“生日”;
- 另一类是不相关特征,例如疾病预测的时候引入的“保险状况”。
这种从d维特征到d’维特征的subset-transform 称为Feature Selection,最终使用这些d’维的特征进行模型训练。
特征选择的优缺点:
| 优点 | 缺点 |
|---|---|
| 提高效率,特征越少,模型越简单 | 筛选特征的计算量较大 |
| 正则化,防止特征过多出现过拟合 | 容易选到无关特征,解释性差 |
| 去除无关特征,保留相关性大的特征,解释性强 |
值得一提的是,在decision tree中,我们使用的decision stump切割方式也是一种feature selection。
那么,如何对许多维特征进行筛选呢?我们可以通过计算出每个特征的重要性(即权重),然后再根据重要性的排序进行选择即可。这种方法在线性模型中比较容易计算。因为线性模型的score是由每个特征经过加权求和而得到的,而加权系数的绝对值|wi|正好代表了对应特征$a_i$的重要性为多少。|wi|越大,表示对应特征$x_i$越重要,则该特征应该被选择。$w$的值可以通过对已有的数据集(xi,yi)建立线性模型而得到。
然而,对于非线性模型来说,因为不同特征可能是非线性交叉在一起的,所以计算每个特征的重要性就变得比较复杂和困难。例如,Random Forest就是一个非线性模型,接下来,我们将讨论如何在RF下进行特征选择。
RF中,特征选择的核心思想是random test。random test的做法是对于某个特征,如果用另外一个随机值替代它之后的表现比之前更差,则表明该特征比较重要,所占的权重应该较大,不能用一个随机值替代。相反,如果随机值替代后的表现没有太大差别,则表明该特征不那么重要,可有可无。所以,通过比较某特征被随机值替代前后的表现,就能推断出该特征的权重和重要性。
那么random test中的随机值如何选择呢?通常有两种方法:
- 使用均匀或者高斯分布抽取随机值替换原特征;
- 通过permutation的方式将原来的所有N个样本的第i个特征值重新打乱分布(相当于重新洗牌)。
比较而言,第二种方法更加科学,保证了特征替代值与原特征的分布是近似的(只是重新洗牌而已)。这种方法叫做permutation test(随机排序测试),即在计算第i个特征的重要性的时候,将N个样本的第i个特征重新洗牌,然后比较演算法在$D$和$D^p$表现的差异性。如果差异很大,则表明第i个特征是重要的。
知道了permutation test的原理后,接下来要考虑的问题是如何衡量performance,即替换前后的表现。显然,我们前面介绍过performance可以用$E_{oob}(G)$来衡量。但是,对于N个样本的第i个特征值重新洗牌重置的$D^p$,要对它进行重新训练,而且每个特征都要重复训练,然后再与原$D$的表现进行比较,过程非常繁琐。为了简化运算,RF的作者提出了一种方法,就是把permutation的操作从原来的training上移到了OOB validation上去,记为$E_{oob}(G^{(p)})$→$E_{oob}^{(p)}(G)$。也就是说,在训练的时候仍然使用$D$,但是在OOB验证的时候,将所有的OOB样本的第i个特征重新洗牌,验证$G$的表现。这种做法大大简化了计算复杂度,在RF的feature selection中应用广泛。
Random Forest in Action
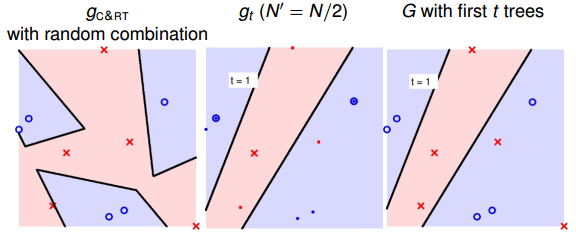
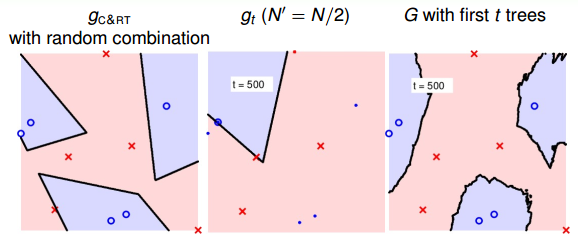
最后,我们通过实际的例子来看一下RF的特点。首先,仍然是一个二元分类的例子。如下图所示,左边是一个C&RT树没有使用bootstrap得到的模型分类效果,其中不同特征之间进行了随机组合,所以有斜线作为分类线;中间是由bootstrap(N’=N/2)后生成的一棵决策树组成的随机森林,图中加粗的点表示被bootstrap选中的点;右边是将一棵决策树进行bagging后的分类模型,效果与中间图是一样的,都是一棵树。
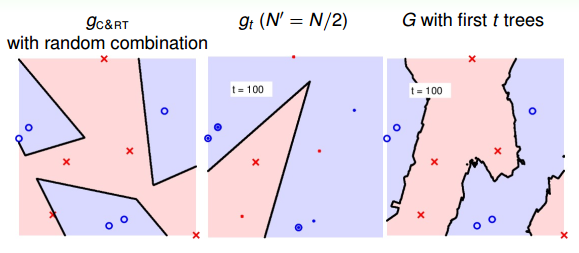
当t=100,即选择了100棵树时,中间的模型是第100棵决策树构成的,还是只有一棵树;右边的模型是由100棵决策树bagging起来的,如下图所示:
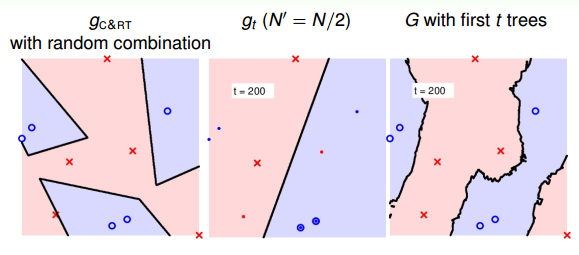
当t=200时:
当t=500时:
当t=800时:
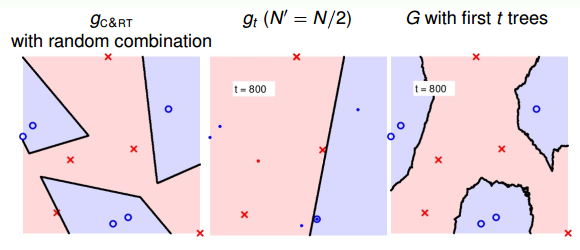
随着树木个数的增加,我们发现,分界线越来越光滑而且得到了large-margin-like boundary,类似于SVM一样的效果。也就是说,树木越多,分类器的置信区间越大。
我们发现RF中,树的个数越多,模型越稳定越能表现得好。在实际应用中,应该尽可能选择更多的树。值得一提的是,RF的表现同时也与random seed有关,即随机的初始值也会影响RF的表现。
总结
本节课主要介绍了Random Forest算法模型。RF将bagging与decision tree结合起来,通过把众多的决策树组进行组合,构成森林的形式,利用投票机制让$G$表现最佳,分类模型更稳定。其中为了让decision tree的随机性更强一些,可以采用randomly projected subspaces操作,即将不同的features线性组合起来,从而进行各式各样的切割。同时,我们也介绍了可以使用OOB样本来进行self-validation,然后可以使用self-validation来对每个特征进行permutaion test,得到不同特征的重要性,从而进行feature selection。总的来说,RF算法能够得到比较平滑的边界,稳定性强,前提是有足够多的树。