Hoeffding不等式
Hoeffding不等式是关于一组随机变量均值的概率不等式。 如果$X$为一组独立同分布的参数为p的伯努利分布随机变量,n为随机变量的个数。定义这组随机变量的均值为:
$$
\bar{X}=\frac{X_{1}+X_2+\cdots +X_{n}}{n}
$$
对于任意的n,Hoeffding不等式可以表示为
$$
P(|\bar{X}-E(\bar{X})|\geqslant \delta )\leqslant exp(-2\delta ^2n^2)
$$
VC维
connecting to learning
基于hoeffding不等式,我们得到下面式子:
$$
P(|E_{in}(h)-E_{out}(h)>\epsilon |)\leqslant 2exp(-2\epsilon ^2N)
$$
其中,$E_{in}(h)$为假设$h$在已知数据集上的表现,$E_{out}(h)$为假设$h$在未知数据集上的表现。
根据上面不等式,我们可以推断,当样本数量N足够大时,$E_{in}(h)$和$E_{out}(h)$将非常接近。
注意在上面推导中,我们是针对某一个特定的假设$h(x)$。在我们的假设空间H中,往往有很多个假设函数(甚至于无穷多个),这里我们先假定$\mathcal{H}$中有M个假设函数。
那么对于整个假设空间$\mathcal{H}$,也就是这M个假设函数,可以推导出下面不等式:
$$
P(|E_{in}(h_1)-E_{out}(h_1)|>\epsilon \cup |E_{in}(h_2)-E_{out}(h_2)|>\epsilon \cdots \cup |E_{in}(h_m)-E_{out}(h_m)|>\epsilon)\\
\leq P(|E_{in}(h_1)-E_{out}(h_1)|>\epsilon)+P(|E_{in}(h_2)-E_{out}(h_2)|>\epsilon)+\cdots +P(|E_{in}(h_m)-E_{out}(h_m)|>\epsilon)\\
\leq 2Mexp(-2\epsilon ^2N)
$$
上面式子的含义是:在假设空间$\mathcal{H}$中,设定一个较小的值$\epsilon$,任意一个假设h,它的$E_{in}(h)$与$E_{out}(h)$的差由该值所约束住。注意这个bound值与 “样本数N和假设数M” 密切相关。
机器学习的两个核心条件
- $E_{in}(g)$与$E_{out}(g)$ 足够接近
- $E_{in}(g)$足够小
上面这两个核心条件,也正好对应着test和train这两个过程。train过程希望损失期望(即$E_{in}(g)$)尽可能小;test过程希望在真实环境中的损失期望也尽可能小,即$E_{in}(g)$与$E_{out}(g)$ 足够接近
但往往我们更多在关心,如何基于模型的假设空间,利用最优化算法,找到Ein最小的解g。但容易忽视test这个过程,如果让学习可行,不仅仅是要在训练集表现好,在真实环境里也要表现好。
从上述推导出来的不等式,我们看到假设数M 在这两个核心条件中有着重要作用。
$$
P(|E_{in}(g)-E_{out}(g)>\epsilon |)\leqslant 2Mexp(-2\epsilon ^2N)
$$
M太小,当N足够大时,$E_{in}(g)$与$E_{out}(g)$比较接近,但如果候选假设集太小,不容易在其中找到一个g,使得$E_{in}(g)$约等于0,第二个条件不能满足。而 如果M太大,这时候选集多了,相对容易在其中找到一个g,使得$E_{in}(g)$约等于0,但第一个条件就不能满足了。所以假设空间$\mathcal{H}$的大小M很关键。
对于一个假设空间,M可能是无穷大的。要能够继续推导下去,那么有一个直观的思路,能否找到一个有限的因子$m_\mathcal{H}$来替代不等式bound中的M。
$$
P(|E_{in}(g)-E_{out}(g)>\epsilon |)\leqslant 2m_\mathcal{H}exp(-2\epsilon ^2N)
$$
虽说假设空间很大,上述推导里,我们用到了$P(h_1 \ or\ h_2 … h_m) <= P(h_1) + P(h_2) + … + P(h_m)$。但事实上,多个h之间并不是完全独立的,他们是有很大的重叠的,也就是在M个假设中,可能有一些假设可以归为同一类。
下面我们以二维假设空间为例,来解释一下该空间下各假设在确定的训练样本上的重叠性。
举例来说,如果我们的算法要在平面上(二维空间)挑选一条直线方程作为g,用来划分一个点x1。假设空间H是所有的直线,它的size M是无限多的。但是实际上可以将这些直线分为两类,一类是把x1判断为正例的,另一类是把x1判断为负例的。如下图所示:
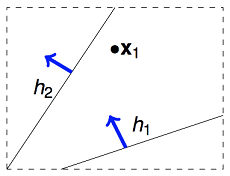
那如果在平面上有两个数据点x1,x2,这样的话,假设空间H中的无数条直线可以分为4类。那依次类推,3个数据点情况下,H中最多有8类直线。4个数据点,H中最多有14类直线(注意:为什么不是16类直线)。
从上面在二维假设空间中的分析,我们可以推测到一个结论,假设空间size M是很大,但在样本集D上,有效的假设函数数目是有限的。接下来我们将继续推导这个有效的假设函数值。
### 假设空间$\mathcal{H}$中的有效假设个数
对于这个有效的假设函数值,我们尝试用一个数学定义来说明:
从$\mathcal{H}$中任意选择一个方程h,让这个h对样本集合D进行二元分类,输出一个结果向量,这样每个输出向量我们称为一个dichotomy。例如在平面里用一条直线对2个点进行二元分类,输出可能为{1,–1},{–1,1},{1,1},{–1,–1},即产生了4个dichotomy。
注意到,如果对平面上的4个点来分类,根据前面分析,输出的结果向量只有14种可能,即有14个dichotomies。如果有N个样本数据,那么有效的假设个数定义为:
effective(N) = H作用于样本集D“最多”能产生多少不同的dichotomy
所以有一个直观思路,能否用effective(N)来替换hoeffding不等式中的M。接下来我们来分析下effective(N)。
$$
P(|E_{in}(g)-E_{out}(g)>\epsilon |)\leqslant 2\cdot effective(N)\cdot exp(-2\epsilon ^2N)
$$
Growth Function
H作用于D“最多”能产生多少种不同的dichotomies?这个数量与假设空间H有关,跟数据量N也有关。将H作用于D“最多”能产生的dichotomies数量(即effective(N) )表示为数学符号:max_H(x1,x2,…,xN)
这个式子又称为“成长函数”(growth function)。在H确定的情况下,growth function是一个与N相关的函数。
下图举4个例子,分别计算其growth function:
| $\mathcal{H}$ | Growth Function |
|---|---|
| Positive rays | N+1 |
| positive intervals | $\binom |
| Convex sets | $2^{n}$ |
| 2D perceptrons | <$2^{n}$ |
求解出$m_\mathcal{H}(N)$后,那是不是可以考虑用$m_\mathcal{H}(N)$替换M? 如下所示:
$$
P(|E_{in}(g)-E_{out}(g)>\epsilon |)\leqslant 2\cdot m_\mathcal{H}(N)\cdot exp(-2\epsilon ^2N)
$$
Break point 与shatter
Shatter的概念:当$\mathcal{H}$作用于有N个inputs的$D$时,产生的dichotomies数量等于这N个点的排列组合数$2^N$时,我们就称这N个inputs被$\mathcal{H}$给shatter掉了。
要注意到 shatter 的原意是“打碎”,在此指“N个点的所有(碎片般的)可能情形都被$\mathcal{H}$产生了”。所以$m_\mathcal{H}(N)=2^N$的情形是即为“shatter”。
对于给定的成长函数$m_\mathcal{H}(N)$,从N=1出发,N慢慢变大,当增大到k时,出现$m_\mathcal{H}(N)<2^N$的情形,则我们说k是该成长函数的break point。对于任何N > k个inputs而言,$\mathcal{H}$都没有办法再shatter他们了。
举例来说,对于上面的positive ray的例子,因为$m_\mathcal{H}(N)=N+1$,当N=2时,$m_\mathcal{H}(N)<2^2$, 所以它的break point就是2。
VC bound
有些$\mathcal{H}$的成长函数很容易找到,比如前面说到的Positive Rays、Positive Intervals以及Convex Sets;有些$\mathcal{H}$则没有那么容易,比如2D perceptrons,我们无法直接看出它的成长函数是什么,那么我们对于这样的$\mathcal{H}$就没辙了吗?也不完全是,至少我们手上还掌握着它的break point,能不能用这个break point干点事呢?如果没办法得到成长函数,能得到成长函数的upper bound也是不错的。
对于存在break point k的成长函数而言,有:
$$
m_\mathcal{H}(N)<\sum_{i=0}^{k-1}\binom{N}{i}
$$
这个式子显然是多项式的,多项式的最高幂次项为:$N^{k–1}$。
所以我们得到结论:如果break point存在(有限的正整数),生长函数$m_\mathcal{H}(N)$是多项式的。
再重复一遍,$\mathcal{H}$作用于数据量为N的样本集D,假设$h$的数量看上去是无穷的,但真正有效(effective)的假设的数量却是有限的,这个数量为$m_\mathcal{H}(N)$。$\mathcal{H}$中每一个$h$作用于$D$都能算出一个$E_{in}$来,一共有$m_\mathcal{H}(N)$个不同的$E_{in}$。
最后我们得到下面的VC bound:
$$
P\left [ \exists h \in \mathcal{H} \ s.t.\ |E_{in}(g)-E_{out}(g)>\epsilon | \right ]
\\leqslant 4\cdot m_\mathcal{H}(2N)\cdot exp(-\frac{1}{8}\epsilon ^2N)
$$
关于这个公式的数学推导,我们可以暂且不去深究。我们先看一下这个式子的意义,如果假设空间存在有限的break point,那么$m_\mathcal{H}(N)$会被最高幂次为k–1的多项式上界给约束住。随着N的逐渐增大,指数式的下降会比多项式的增长更快,所以此时VC Bound是有限的。更深的意义在于,N足够大时,对H中的任意一个假设h,$E_{in}(h)$都将接近于$E_{out}(h)$,这表示学习可行的第一个条件是有可能 成立的。
总结
说了这么多,VC维终于露出庐山真面目了。
一个假设空间H的VC dimension,是这个H最多能够shatter掉的点的数量,根据定义,可以得到一个明显的结论:k=d_vc +1
根据前面的推导,我们知道VC维的大小:与学习算法A无关,与输入变量X的分布也无关,与我们求解的目标函数f 无关。它只与模型和假设空间有关。
我们已经分析了,对于2维的perceptron,它不能shatter 4个样本点,所以它的VC维是3。此时,我们可以分析下2维的perceptron,如果样本集是线性可分的,perceptron learning algorithm可以在假设空间里找到一条直线,使$E_{in}(g)=0$;另外由于其VC维=3,当N足够大的时候,可以推断出:$E_{out}(g)$约等于 $E_{in}(g)$。这样学习可行的两个条件都满足了,也就证明了2维感知器是可学习的。
回到最开始提出的学习可行的两个核心条件,尝试用VC维来解释:
- $E_{in}(g)$与$E_{out}(g)$ 足够接近
- $E_{in}(g)$足够小
当VC维很小时,条件1容易满足,但因为假设空间较小,可能不容易找到合适的g 使得$E_{in}(g)=0$。当VC维很大时,条件2容易满足,但条件1不容易满足,因为VC bound很大。
VC维反映了假设空间H 的强大程度(powerfulness),VC 维越大,H也越强,因为它可以打散(shatter)更多的点。
定义模型自由度是,模型当中可以自由变动的参数的个数,即我们的机器需要通过学习来决定模型参数的个数。
一个实践规律:VC 维与假设参数w 的自由变量数目大约相等。d_VC = #free parameters。
模型越复杂,VC维大,$E_{out}(g)$可能距离$E_{in}(g)$越远。如下图所示,随着d_vc的上升,$E_{in}(g)$不断降低,而模型复杂度不断上升。

模型较复杂时(d_vc 较大),需要更多的训练数据。 理论上,数据规模N 约等于10000$d_{vc}$(称为采样复杂性,sample complexity)。然而,实际经验是,只需要
N = 10$d_{vc}$。 造成理论值与实际值之差如此之大的最大原因是,VC Bound 过于宽松了,我们得到的是一个比实际大得多的上界。
注意在前述讨论中,理想的目标函数为f(x),error measure用的是“0–1 loss”。如果在unknown target上引入噪声(+noise),或者用不同的error measure方法,VC theory还有效吗?这里只给出结论,VC theory对于绝大部分假设空间(or 加入噪声)和error度量方法,都是有效的。
除此外,我们为了避免overfit,一般都会加正则项。那加了正则项后,新的假设空间会得到一些限制,此时新假设空间的VC维将变小,也就是同样训练数据条件下,Ein更有可能等于Eout,所以泛化能力更强。这里从VC维的角度解释了正则项的作用。
参考
林轩田 机器学习基石