XGBoost
xgb本质上仍然是梯度提升树。xgb对应的模型就是一堆cart树,也就是一堆的if else。
xgboost为什么使用CART树而不是用普通的决策树呢?
简单讲,对于分类问题,由于CART树的叶子节点对应的值是一个实际的分数,而非一个确定的类别,这将有利于实现高效的优化算法。xgboost出名的原因一是准,二是快,之所以快,其中就有选用CART树的一份功劳。
模型
xgboost模型的数学表示为:
$$
\hat{y_i}=\sum_{m=1}^{M}f_m(x_i),f_m\in\mathcal{F}
$$
这里的M就是树的棵数,$\mathcal{F}$表示所有可能的CART树,$f_m$表示一棵具体的CART树。这个模型由M棵CART树组成,模型的参数就是这M棵CART树的参数。
目标函数
采用结构风险最小化的策略,模型的目标函数为
$$
obj(\theta)=\sum_{i=1}^{n}l(y_i,\hat{y_i})+\sum_{m=1}^{M}\Omega (f_m)
$$
这个目标函数包含两部分,第一部分就是损失函数,第二部分就是正则项,这里的正则化项由K棵树的正则化项相加而来。
前向分步算法
由式(2)可以看到,xgb是一个加法模型,根据前向分步算法,我们不直接优化整个目标函数,而是分步骤优化目标函数,首先优化第一棵树,完了之后再优化第二棵树,直至优化完M棵树
第t步时,在现有的t-1棵树的基础上,找到使得目标函数最小的那棵CART树,即为第t棵树
$$
\begin {align}
obj^{(t)}&=\sum_{i=1}^{n}l(y_i,\hat{y_i}^{(t)})+\sum_{m=1}^{t}\Omega (f_m)\\
&=\sum_{i=1}^{n}l(y_i,\hat{y_i}^{(t-1)}+f_t(x_i))+\Omega (f_t)+\sum_{m=1}^{t-1}\Omega (f_m)\\
&=\sum_{i=1}^{n}l(y_i,\hat{y_i}^{(t-1)}+f_t(x_i))+\Omega (f_t)+constant
\end {align}
$$
上式中的constant就是前t-1棵树的复杂度
借鉴GBDT的梯度提升思想,对于一般的损失函数$l(y_i, \hat{y_i})$来说,我们对$l(y_i, \hat{y_i})$在当前模型$f(x)=\sum_{m=1}^{t-1}f_m(x)$处做二阶泰勒展开,
$$
obj^{(t)}=\sum_{i=1}^{n}[l(y_i,\hat{y_i}^{(t-1)})+g_if_t(x_i)+\frac{1}{2}h_if^2_t(x_i)]+\Omega (f_t)+constant
$$
其中,
$$
\begin{align}
g_i=\frac{\partial l(y_i,\hat{y_i}^{(t-1)})}{\partial \hat{y_i}^{(t-1)}}\\
h_i=\frac{\partial^2 l(y_i,\hat{y_i}^{(t-1)})}{\partial (\hat{y_i}^{(t-1)})^2}\
\end{align}
$$
分别表示损失函数在当前模型的一阶导和二阶导,每一个样本都可以计算出该样本点的$g_i$和$h_i$,而且样本点之间的计算可以独立进行,互不影响,也就是说,可以并行计算。
对式(3)进行化简,去掉与$f_t(x)$无关的项,得到
$$
obj^{(t)}=\sum_{i=1}^{n}[g_if_t(x_i)+\frac{1}{2}h_if^2_t(x_i)]+\Omega (f_t)
$$
式(4)就是每一步要优化的目标函数。
重写优化函数
每一步学到的CART树可以表示成
$$
f_m(x) = w_{q(x)} , w \in R^T , q : R^d \rightarrow { 1,2,...,T }
$$
其中T为叶子节点个数,q(x)是一个映射,用来将样本映射成1到T的某个值,也就是把它分到某个叶子节点,q(x)其实就代表了CART树的结构。$w_q(x)$自然就是这棵树对样本x的预测值了。
因此,树的复杂度可以表示为:
$$
\Omega(f)=\gamma T+\frac{1}{2}\lambda \sum_{j=1}^{T}w_j^2
$$
$\gamma $和$\lambda$ 越大,树越简单。
为什么xgboost要选择这样的正则化项?很简单,好使!效果好才是真的好。
将复杂度代入式(4)并做变形,得到
$$
\begin{align}
obj^{(t)}&=\sum_{i=1}^{n}[g_iw_{q(x_i)}+\frac{1}{2}h_iw^2_{q(x_i)}]+\gamma T+\frac{1}{2}\lambda \sum_{j=1}^{T}w_j^2\\
&=\sum_{j=1}^{T}[(\sum_{i\in I_j}g_i)w_j+\frac{1}{2}(\sum_{i\in I_j}h_i+\lambda)w_j^2]+\gamma T
\end{align}
$$
$I_j$代表一个集合,集合中每个值代表一个训练样本的序号,整个集合就是被第t棵CART树分到了第j个叶子节点上的所有训练样本。令$G_j=\sum_{i\in I_j}g_i$和$H_j=\sum_{i\in I_j}h_i$
$$
obj^{(t)}=\sum_{j=1}^{T}[G_jw_j+\frac{1}{2}(H_j+\lambda)w_j^2]+\gamma T
$$
对于第t棵CART树的某一个确定的结构(可用q(x)表示),所有的Gj和Hj都是确定的。而且上式中各个叶子节点的值wj之间是互相独立的。上式其实就是一个简单的一元二次式,我们很容易求出各个叶子节点的最佳值以及此时目标函数的值。如下所示:
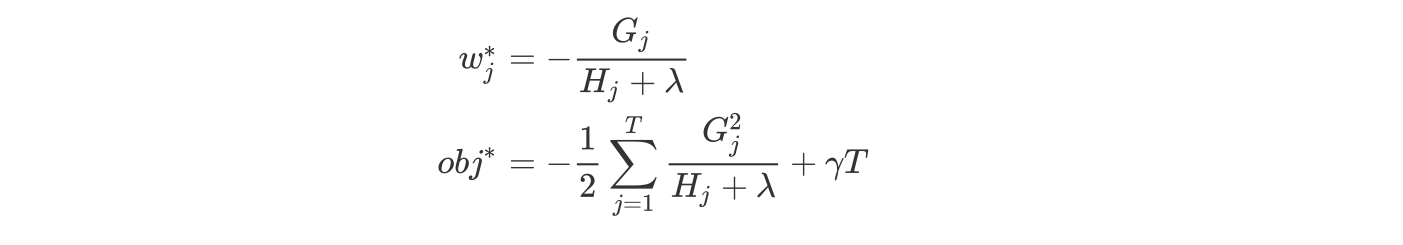
$obj$表示了这棵树的结构有多好,值越小的话,代表这样结构越好!也就是说,它是衡量第t棵CART树的结构好坏的标准。这个值仅仅是用来衡量结构的好坏的,与叶子节点的值是无关的,因为obj*只和Gj和Hj和T有关,而它们又只和树的结构(q(x))有关,与叶子节点的值可是半毛关系没有。
Note:这里,我们对$w_j$给出一个直觉的解释,以便能获得感性的认识。我们假设分到j这个叶子节点上的样本只有一个。那么,$w_j$就变成如下这个样子:
$$
w_j=\underbrace{\frac{1}{h_j+\lambda}}_{学习率}\cdot \underbrace{-g_j}_{负梯度}
$$
这个式子告诉我们,$w_j^*$的最佳值就是负的梯度乘以一个权重系数,该系数类似于随机梯度下降中的学习率。观察这个权重系数,我们发现,$h_j$越大,这个系数越小,也就是学习率越小。$h_j$越大代表什么意思呢?代表在该点附近梯度变化非常剧烈,可能只要一点点的改变,梯度就从10000变到了1,所以,此时,我们在使用反向梯度更新时步子就要小而又小,也就是权重系数要更小。
找出最优树结构
好了,有了评判树的结构好坏的标准,我们就可以先求最佳的树结构,这个定出来后,最佳的叶子结点的值实际上在上面已经求出来了。
问题是:树的结构近乎无限多,一个一个去测算它们的好坏程度,然后再取最好的显然是不现实的。所以,我们仍然需要采取一点策略,这就是逐步学习出最佳的树结构。这与我们将M棵树的模型分解成一棵一棵树来学习是一个道理,只不过从一棵一棵树变成了一层一层节点而已。
具体来说,对于特征集中每一个特征$a$, 找出该特征的所有切分点,对每一个确定的切分点,我们衡量切分好坏的标准如下:
$$
Gain=\frac{1}{2}[\frac{G_L^2}{H_L+\lambda}+\frac{G_R^2}{H_R+\lambda}-\frac{(G_L+G_R)^2}{H_L+H_R+\lambda}]-\gamma
$$
这个Gain实际上就是单节点的obj减去切分后的两个节点的树obj,Gain如果是正的,并且值越大,表示切分后obj越小于单节点的obj,就越值得切分。同时,我们还可以观察到,Gain的左半部分如果小于右侧的$\gamma$,则Gain就是负的,表明切分后obj反而变大了。$\gamma$在这里实际上是一个临界值,它的值越大,表示我们对切分后obj下降幅度要求越严。这个值也是可以在xgboost中设定的。
扫描结束后,我们就可以确定是否切分,如果切分,对切分出来的两个节点,递归地调用这个切分过程,我们就能获得一个相对较好的树结构。
注意:xgboost的切分操作和普通的决策树切分过程是不一样的。普通的决策树在切分的时候并不考虑树的复杂度,而依赖后续的剪枝操作来控制。xgboost在切分的时候就已经考虑了树的复杂度,就是那个γ参数。所以,它不需要进行单独的剪枝操作。
GBDT和XGBOOST区别
- gbdt以CART作为基分类器,xgb还支持线性分类器,这个时候xgb相当于带L1和L2正则项的LR或线性回归,(带正则可以控制模型的复杂度)
- gbdt在优化时只用到一阶导数,xgb则对代价函数进行了二阶泰勒展开,同时用到了一阶和二阶导数。
- Shrinkage(缩减),相当于学习速率(xgb中的eta),xgb在进行完一次迭代后,会将叶子节点的权重乘上该系 数,主要是为了削弱各棵树的影响,让后面有更大的学习空间
- 列抽样(column subsampling),xgb借鉴了rf的做法,支持列抽样,不仅能降低过拟合,还能减少计算。
- 对于特征的值有缺失的样本,xgb可以自动学习出它的分裂方向。
- 在特征粒度上可以并行处理。在训练之前,预先对每个特征内部进行了排序找出候选切割点,然后保存为block结构,后面的迭代中重复地使用这个结构,大大减小计算量。在进行节点的分裂时,需要计算每个特征的增益,最终选增益最大的那个特征去做分裂,那么各个特征的增益计算就可以开多线程进行,即在不同的特征属性上采用多线程并行方式寻找最佳分割点。
- 用贪心法枚举所有可能的分割点,当数据无法一次载入内存或者在分布式情况下,贪心算法效率就会变得很低,所以xgboost还提出了一种可并行的近似直方图算法,用于高效地生成候选的分割点。
思考
Q:xgb怎么处理缺失值?
A:xgb处理缺失值的方法和其他树模型不同,xgboost把缺失值当做稀疏矩阵来对待,本身的在节点分裂时不考虑的缺失值的数值。缺失值数据会被分到左子树和右子树分别计算损失,选择较优的那一个。如果训练中没有数据缺失,预测时出现了数据缺失,那么默认被分类到右子树。
PS:随机森林怎么处理缺失值?
- 数值型变量用中值代替,类别型变量用众数代替。
- 引入了权重。即对需要替换的数据先和其他数据做相似度测量,补全缺失点是相似的点的数据会有更高的权重W
Q:xgb为什么用二阶展开项?
A:好用?得到关于梯度更多的信息.?
二阶导反映了梯度变化的情况,二阶导越大,梯度变化越剧烈,那么学习的时候越需要小心!!!
Q:如何保证一元二次式(7)是开口向上的呢?即如果$\frac{1}{2}(H_j+\lambda)<0$,那么不是岂可以使损失函数达到无限小?
A:感谢zwt同学!要知道,$H_j=\sum_{i\in I_j}h_i$,其中每一个$h_i$表示损失函数对当前预测值的二阶导,这个二阶导数值一定是大于0的,因为如果二阶导不大于0,那么损失函数就不是凸函数,也就没有最小值,(损失函数要大于0),而xgb要求自定义损失函数要二阶可导,因此二阶导数值必须要大于0
Q:xgb多分类是怎么处理的?每个类别的概率是怎么来的!!!!!????
A:one vs all 有n个类别,就训练n个模型,最后将这n个模型的输出做softmax归一化
特征分裂点查找算法
- 贪心法
对于特征集中每一个特征$a$, 对每一个确定的切分点,都计算得分,选择得分最高的特征对应的划分点。
这种完全贪心算法,贪婪的遍历所有的切分点,当所有的数据点不能全部加载到内存时,算法就会变的低效。同时在XGBoost分布式学习时也会遇到这样的问题。所以此时需要一些近似算法来获取切分点列表。
- 近似法
XGBoost中的近似方法框架

算法讲解: 前面一个for循环做的工作是,对特征K根据该特征分布的分位数找到切割点的候选集合Sk={sk1,sk2,...,skl},这样做的目的是提取出部分的切分点不用遍历所有的切分点。其中获取某个特征K的候选切割点的方式叫proposal.主要有两种proposal方式:global proposal和local proposal. 第二个for循环的工作是,将每个特征的取值映射到由这些该特征对应的候选点集划分的分桶(buckets)区间{skv≥xjk>skv−1}中,对每个桶(区间)内的样本统计值G、H进行累加统计,最后在这些累计的统计量上寻找最佳分裂点。这样做的主要目的是获取每个特征的候选分割点的G和H量。
问题1.如何根据特征分布的分位数挑选出候选点集??
问题2.global proposal和local proposal有什么不同??
注:分位点即对一组数据排序后前百分之多少的点所处的位置,0.25-quantile(0.25分位点的数),即取出rank为0.25*N的数
加权分位点
首先将数据根据大小排序,然后根据每个点的权重确定rank,例如
| input | 1 | 2 | 4 | 6 | 9 |
|---|---|---|---|---|---|
| weight | 0.1 | 0.3 | 0.4 | 0.15 | 0.05 |
| rank | 0.1 | 0.4 | 0.8 | 0.95 | 1 |
如果不是加权的话(即weight都相同),那么就是
| input | 1 | 2 | 4 | 6 | 9 |
|---|---|---|---|---|---|
| weight | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 |
| rank | 0.2 | 0.4 | 0.6 | 0.8 | 1 |
也就是不加权的rank,相邻点的rank步长固定,都是0.2
不加权之前4是0.6分位点,加权之后分位点为0.8
分位数缩略图(Quantile Sketch)
$\varepsilon -approximate$分位点
原因: 当一个序列无法全部加载到内存时,常常采用分位数缩略图近似的计算分位点来近似获取特定的查询。
假定序列的大小为N,给定误差ε和rank=r,其ε−approximate分位点为序列中的一些元素,且这些元素的rank值r′满足:$r′∈[r−εN,r+εN]$。以下面的序列为例,给定$ε=0.1,ϕ=0.5$,此时r=0.5×16=8,则rank值在区间[6.2,9.6][6.2,9.6]的元素为:{6,7,8},即: 0.1-appoximate 0.5-quantile为:{6,7,8}

quantile summary
ε-approximate quantile summary 是一种数据结构,该数据结构能够以 $εN$的精度计算任意的分位查询。当一个序列无法全部加载到内存时,常常采用quantile suammary近似的计算分位点。
下图展示了上面序列的一个quantile suammary,可以看出:quantile summary中value是原序列的一个子集,通过这种方式就能达到减少数据量的效果。
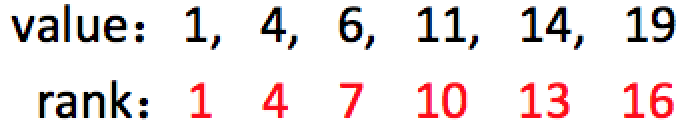
近似算法中的分位数缩略图(Weighted Quantile Sketch)
对于第k个特征,我们用一个multi-set: Dk=(x1k,h1),(x2k,h2),…(xnk,hn),来表示每个训练实例的第k个特征值以及它的二阶梯度值统计。其中hi表示i个实例的第k个特征值对应的二阶梯度值统计,可看作i个实例的第k个特征值的权重。
有了权重后,就可以根据Rank函数$r_k(z)=\frac{1}{\sum_{(x,h) \in D_k}h}\sum_{(x,h)\in D_k,x<z}^{}h$,这个Rank函数跟之前的例子是吻合的,算出每个样本实例的rank,该Rank函数,输入为某个特征值z,计算的是该特征所有可取值中小于z的特征值的总权重占总的所有可取值的总权重和的比例,输出为一个比例值。于是我们就能用下面这个不等式来寻找候选分离点{sk1,sk2,sk3,⋅,⋅,skl}
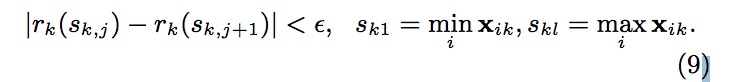
其中sk1是特征k的取值中最小的值xik,其中skl是特征k的取值中最大的值xik,这是分位数缩略图的要求需要保留原序列中的最小值和最大值。ϵ是一个近似比例,或者说是扫描步幅。可以理解为在特征K的取值范围上,按照步幅ϵ挑选出特征K的取值候选点,组成候选点集。起初是从sk1起,每次增加ϵ∗(skl−sk1)作为候选点,加入到候选集中。如此计算的话,这意味着大约是 1/ϵ个候选点。 此时特征k的取值中最小的值xik和特征k的取值中最大的值xik来自的数据集Dk,对于Dk的数据集有两种定义,一种是一开始选好,然后每次树切分都不变,也就是说是在总体样本里选最大值skl和最小值sk1,这就是我们之前定义的global proposal。另外一种是树每次确定好切分点的分割后样本也需要进行分割,最大值skl和最小值sk1来自子树的样本集Dk,这就是local proposal
为什么可以用二阶梯度的值$h_i$表示权重呢?
$w_j$的最佳值就是负的梯度乘以一个权重系数,该系数类似于随机梯度下降中的学习率。观察这个权重系数,我们发现,$h_j$越大,这个系数越小,也就是学习率越小。$h_j$越大代表什么意思呢?代表在该点附近梯度变化非常剧烈,可能只要一点点的改变,梯度就从10000变到了1,所以,此时,我们在使用反向梯度更新时步子就要小而又小,也就是权重系数要更小。
分布式加权分位数缩略图:对于需要并行的获取候选集切割点,需要使用分布式加权分位数缩略图,必须包含两个操作merge和prune。